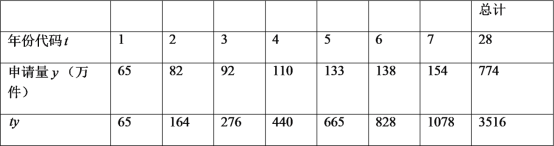题目内容
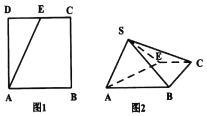
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.
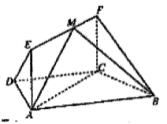
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(Ⅰ)在梯形![]() 中,设
中,设![]() ,题意求得
,题意求得![]() ,再由余弦定理求得
,再由余弦定理求得![]() ,满足
,满足![]() ,得则
,得则![]() .再由
.再由![]() 平面
平面![]() 得
得![]() ,由线面垂直的判定可.进一步得到
,由线面垂直的判定可.进一步得到![]() 丄平面
丄平面![]() ;(Ⅱ)分别以直线
;(Ⅱ)分别以直线![]() 为:
为:![]() 轴,
轴,![]() 轴轴建立如图所示的空间直角坐标系,设
轴轴建立如图所示的空间直角坐标系,设![]() ,令
,令![]()
![]() 得到
得到![]() 的坐标,求出平面
的坐标,求出平面![]() 的一法向量.由题意可得平面的
的一法向量.由题意可得平面的![]() 一个法向量,求出两法向量所成角的余弦值,可得当
一个法向量,求出两法向量所成角的余弦值,可得当![]()
![]() 时,有最小值为
时,有最小值为![]() ,此时点
,此时点![]() 与点
与点![]() 重合.
重合.
试题解析:(Ⅰ)证明:在梯形![]() 中,∵
中,∵![]() ,设
,设![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() .则
.则![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,而
,而![]() ,∴
,∴![]() 平面
平面![]() .∵
.∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)解:分别以直线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,

设![]() ,令
,令![]() ,
,
则![]() ,
,
∴![]()
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
由 得
得![]() ,取
,取![]() ,则
,则![]() ,
,
∵![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴
∵![]() ,∴当
,∴当![]() 时,
时,![]() 有最小值为
有最小值为![]() ,
,
∴点![]() 与点
与点![]() 重合时,平面
重合时,平面![]() 与平面
与平面![]() 所成二面角最大,此时二面角的余弦值为
所成二面角最大,此时二面角的余弦值为![]() .
.

【题目】峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:度)分组的频率分布直方图如下图:
(单位:度)分组的频率分布直方图如下图:

若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表:
月平均用电量(度) |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数(同一组中的数据用该组区间的中点值作代表);
(2)(![]() )将“一般用户”和“大用户”的户数填入下面
)将“一般用户”和“大用户”的户数填入下面![]() 的列联表:
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(![]() )根据(
)根据(![]() )中的列联表,能否有
)中的列联表,能否有![]() 的把握认为 “用电量的高低”与“使用峰谷电价”有关?
的把握认为 “用电量的高低”与“使用峰谷电价”有关?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,