题目内容
18.已知数列{an}的第1项a1=1,且an+1=$\frac{a_n}{{1+{a_n}}}(n∈{N^*})$.(1)计算a2,a3,a4;
(2)猜想an的表达式,并用数学归纳法进行证明.
分析 (1)利用递推关系式可求出a2,a3,a4的值.
(2)通过观察归纳出规律,从而猜想其通项公式,即可用数学归纳法证明.
解答 解:(1)由题意可得:a2=$\frac{{a}_{1}}{1+{a}_{1}}$=$\frac{1}{1+1}$=$\frac{1}{2}$,
a3=$\frac{{a}_{2}}{1+{a}_{2}}$=$\frac{\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$,
a4=$\frac{{a}_{3}}{1+{a}_{3}}$=$\frac{\frac{1}{3}}{1+\frac{1}{3}}$=$\frac{1}{4}$…3分
(2)通过观察归纳出规律:其通项应是一个真分数,分子为1,分母与相应的下标相同,故猜想an=$\frac{1}{n}$(n∈N*).…6分
用数学归纳法证明如下:
①当n=1时,猜想显然成立;
②假设当n=k(k∈N*)时猜想成立,即:ak=$\frac{1}{k}$,
那么,ak+1=$\frac{{a}_{k}}{1+{a}_{k}}$=$\frac{\frac{1}{k}}{1+\frac{1}{k}}$=$\frac{1}{k+1}$,
所以,当n=k+1时猜想也成立.
根据①②,可知猜想对任何n∈N*都成立…14分
点评 本题主要考查了数学归纳法的应用,正确理解递推关系并求出数列的前几项和使用归纳推理是解题的关键,属于中档题.

练习册系列答案
相关题目
10.设$\overrightarrow a$是非零向量,λ为负实数,下列结论中正确的是( )
| A. | $\overrightarrow a$与$λ\overrightarrow a$的方向相反 | B. | $|{λ\overrightarrow a}|≥|{\overrightarrow a}|$ | ||
| C. | $\overrightarrow a$与${λ^2}\overrightarrow a$的方向相同 | D. | $|{λ\overrightarrow a}|=|λ|\overrightarrow a$ |
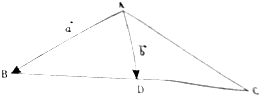 如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.
如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.