题目内容
7.如图是一个算法的流程图,回答下面的问题:当输入的值为3时,输出的结果为20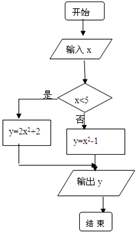
分析 模拟执行程序框图,可得程序框图的功能是计算并输出y=$\left\{\begin{array}{l}{2{x}^{2}+2}&{x<5}\\{{x}^{2}-1}&{x≥5}\end{array}\right.$的值,代入x=3即可得解.
解答 解:模拟执行程序框图,可得程序框图的功能是计算并输出y=$\left\{\begin{array}{l}{2{x}^{2}+2}&{x<5}\\{{x}^{2}-1}&{x≥5}\end{array}\right.$的值,
∵x=3,满足条件x<5,y=20
∴输出y的值为20.
故答案为:20.
点评 本题主要考查了选择结构的程序框图,模拟执行程序框图,得程序框图的功能是解题的关键,属于基础题.

练习册系列答案
相关题目
2.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,其余人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,其余人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.01的前提下,认为休闲方式与性别有关系.独立性检验观察值计算公式$k=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,独立性检验临界值表:
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.01的前提下,认为休闲方式与性别有关系.独立性检验观察值计算公式$k=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,独立性检验临界值表:
| P(K2≥k0) | 0.50 | 0.25 | 0.15 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 0.455 | 1.323 | 2.072 | 3.841 | 5.024 | 6.635 | 7.879 |
19.若数列{an}的前n项和Sn=n2-2n+3,则此数列的前3项依次为( )
| A. | -1,1,3 | B. | 2,3,6 | C. | 6,1,3 | D. | 2,1,3 |
16.为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由.
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由.