题目内容
13.已知${(\sqrt{x}+\frac{2}{x^2})^n}$的展开式中,(1)若第5项的系数与第3项的系数之比是56﹕3,求展开式中的常数项;
(2)求证:二项式${(\sqrt{x}+\frac{2}{x^2})^n}$与${(\sqrt{x}+\frac{2}{x^2})^{n+1}}$的展开式中不可能都有常数项.
分析 (1)在展开式的通项中,令x=1得出第5项的系数与第3项的系数表达式,由已知,求出n,再在通项中令x得指数为0,确定常数项.
(2)假设两个展开式中都含有常数项,根据展开式求出常数项,得到矛盾.
解答 解:展开式的通项为${T}_{k+1}={C}_{n}^{k}•{(\sqrt{x})}^{n-k}•{(\frac{2}{{x}^{2}})}^{k}={C}_{n}^{k}{•2}^{k}{•x}^{\frac{n-5k}{2}}$,
第5项的系数为${C}_{n}^{4}$•24,第3项的系数为${C}_{n}^{2}•{2}^{2}$,
由已知,得出${C}_{n}^{4}$•24:${C}_{n}^{2}•{2}^{2}$=56:3,解得n=10或n=-5(舍),
所以通项公式${T}_{k+1}={C}_{10}^{k}{(\sqrt{x})}^{10-k}{(\frac{2}{{x}^{2}})}^{k}={C}_{10}^{k}{2}^{k}{x}^{5-\frac{5}{2}k}$,
当k=2时,取到常数项 即T3=180.
(2)假设它们的展开式都有常数项,分别为第r+1和k+1项,
则${T}_{r+1}={2}^{r}{C}_{n}^{r}{x}^{\frac{n-5r}{2}}$为常数项,由$\frac{n-5r}{2}=0$得n=5r,即n是5的倍数,
${T}_{k+1}={2}^{k}{C}_{n+1}^{k}{x}^{\frac{n+1-5k}{2}}$为常数项,由$\frac{n+1-5k}{2}$=0得n=5r-1,即n不是5的倍数,两者矛盾,
∴假设不成立,即原命题成立.
点评 本题考查二项式定理的应用:求指定的项.牢记公式是基础,考查学生的运算能力.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.01的前提下,认为休闲方式与性别有关系.独立性检验观察值计算公式$k=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,独立性检验临界值表:
| P(K2≥k0) | 0.50 | 0.25 | 0.15 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 0.455 | 1.323 | 2.072 | 3.841 | 5.024 | 6.635 | 7.879 |
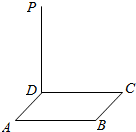 已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8
已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8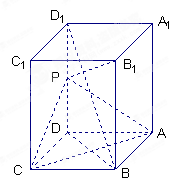 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.