题目内容
13.设函数f(x)=-x3+2x2-x(x∈R).(1)求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)求函数f(x)的极值.
分析 (1)先求出函数f(x)的导数,求出f(2),f′(2)的值,从而求出切线方程;(2)先求出函数的导数,得到函数的单调区间,从而求出函数的极值.
解答 解:(1)因为f(x)=-x3+2x2-x,
所以 f′(x)=-3x2+4x-1,且f(2)=-2,
所以 f′(2)=-5,
所以 曲线f(x)在点(2,-2)处的切线方程是y+2=-5(x-2),
整理得:5x+y-8=0.
(2)由(1)知f′(x)=-3x2+4x-1=-(3x-1)(x-1),
令f′(x)=0,解得:x=$\frac{1}{3}$或x=1,
所以f′(x),f(x)变化情况如下表:
| x | (-∞,-$\frac{1}{3}$) | $\frac{1}{3}$ | ($\frac{1}{3}$,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | -$\frac{4}{27}$ | ↗ | 0 | ↘ |
点评 本题考查了曲线的切线方程,考查函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.由抛物线y=x2与直线y=2x围成的封闭图形的面积为( )
| A. | 8 | B. | $\frac{8}{3}$ | C. | $\frac{4}{3}$ | D. | 4 |
4.函数f(x)=x3+3x2+3x-a的极值点的个数是( )
| A. | 2 | B. | 1 | C. | 0 | D. | 由a确定 |
18.如图1是一个边长为1的正三角形,分别连接这个三角形三边中点,将在三角剖分成4个三角开(如图2),再分别连接图2中一个小三角形三边的中点,又可将原三角形剖分成7个三角形(如图3),…,依此类推,设第n个图中原三角形被剖分成an个三角形,则第4个图中最小三角形的边长为( );a100=( )
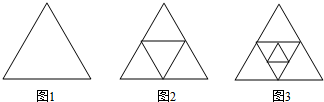

| A. | $\frac{1}{6}$,300 | B. | $\frac{1}{8}$,300 | C. | $\frac{1}{6}$,298 | D. | $\frac{1}{8}$,298 |
19.若数列{an}的前n项和Sn=n2-2n+3,则此数列的前3项依次为( )
| A. | -1,1,3 | B. | 2,3,6 | C. | 6,1,3 | D. | 2,1,3 |
 已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8
已知边长为6的正方形ABCD所在平面外一点P,且PD⊥平面ABCD,PD=8