柱坐标对应的点的直角坐标是$$．题目和参考答案——青夏教育精英家教网——

题目内容

3．柱坐标（2，$\frac{2π}{3}$，1）对应的点的直角坐标是$（-1，\sqrt{3}，1）$．

分析利用柱坐标与直角坐标的关系即可得出．

解答解：柱坐标（2，$\frac{2π}{3}$，1）对应的点的直角坐标是$（2cos\frac{2π}{3}，2sin\frac{2π}{3}，1）$，即$（-1，\sqrt{3}，1）$．
故答案为：$（-1，\sqrt{3}，1）$．

点评本题考查了柱坐标与直角坐标的关系，属于基础题．

练习册系列答案

口算心算速算天天练习簿系列答案

新课程学习与测评高中版系列答案

蓉城学霸系列答案

胜券在握阅读系列答案

新课程实验报告系列答案

新课堂实验报告系列答案

小学生家庭作业系列答案

考易通课时全优练系列答案

与名师对话同步单元测试卷系列答案

黄冈状元笔记系列答案

相关题目

17．在△ABC中，$\frac{{a}^{3}{+b}^{3}{-c}^{3}}{a+b-c}$=c²，sinA•sinB=$\frac{3}{4}$，则△ABC一定是（　　）

	A．	等边三角形		B．	等腰三角形
	C．	直角三角形		D．	等腰三角形或直角三角形

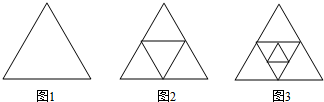
18．如图1是一个边长为1的正三角形，分别连接这个三角形三边中点，将在三角剖分成4个三角开（如图2），再分别连接图2中一个小三角形三边的中点，又可将原三角形剖分成7个三角形（如图3），…，依此类推，设第n个图中原三角形被剖分成a_n个三角形，则第4个图中最小三角形的边长为（　　）；a₁₀₀=（　　）

$\frac{1}{6}$，300

$\frac{1}{8}$，300

$\frac{1}{6}$，298

$\frac{1}{8}$，298

11．二项式${（\root{3}{x}-\frac{3}{x}）^n}$的展开式中含有x²项，则n最小时，展开式中所有系数之和为64．

18．已知数列{a_n}的第1项a₁=1，且a_n+1=$\frac{a_n}{{1+{a_n}}}（n∈{N^*}）$．
（1）计算a₂，a₃，a₄；
（2）猜想a_n的表达式，并用数学归纳法进行证明．

8．复数$\frac{a+i}{1+i}$为纯虚数，其中i为虚数单位，则实数a的值为（　　）

15．判断下列命题的真假，其中全是真命题的组合是（　　）
①若$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow 0$，则A、B、C为一个三角形的三个顶点；
②$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}|是\overrightarrow b=\overrightarrow 0$的充要条件；
③在△ABC中，若$\overrightarrow{AB}•\overrightarrow{BC}＞0$，则△ABC是钝角三角形；
④若$\overrightarrow a$、$\overrightarrow b$均为非零向量，则$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}|•|{\overrightarrow b}|$是$\overrightarrow a∥\overrightarrow b$的充分不必要条件．

12．已知正项等差数列{a_n}的前n项和为S_n，若S₃=12，且2a₁，a₂，a₃+1成等比数列．
（1）求{a_n}的通项公式a_n和S_n；
（2）记b_n=$\frac{a_n}{2^n}$的前n项和T_n，求T_n．

13．已知ω＞0，函数f（x）=sinωx在区间[-$\frac{π}{4}$，$\frac{π}{4}$]上恰有9个零点，那么ω的取值范围为（　　）