题目内容
12.已知关于x的不等式x2-2x+2<2ax+1(a∈R).(1)若此不等式的解集为(b,2),求a+b的值;
(2)若a≥-2,求不等式的解集.
分析 (1)不等式即为x2-(2+2a)x+1<0,由此不等式的解集为(b,2),即有b,2是方程x2-(2+2a)x+1=0的两根,
再由韦达定理,解方程即可得到;
(2)求出方程的判别式,对a讨论,a=0,a>0,-2≤a<0,结合图象和二次不等式的解法,即可得到解集.
解答 解:(1)不等式即为x2-(2+2a)x+1<0,
由此不等式的解集为(b,2),即有b,2是方程x2-(2+2a)x+1=0的两根,
则有b+2=2+2a,2b=1,
解得a=$\frac{1}{4}$,b=$\frac{1}{2}$,
则a+b=$\frac{3}{4}$;
(2)不等式即为x2-(2+2a)x+1<0,
判别式为△=(2+2a)2-4=4a(a+2),
若a=0,则△=0,即为x2-2x+1<0,即有(x-1)2<0,解集为∅;
若-2≤a<0,则△<0,解集为∅;
若a>0,则△>0,x2-(2+2a)x+1=0的两根为x=1+a±$\sqrt{a(a+2)}$,
不等式的解集为(1+a-$\sqrt{a(a+2)}$,1+a+$\sqrt{a(a+2)}$).
综上可得,当-2≤a≤0时,解集为∅;
当a>0时,解集为(1+a-$\sqrt{a(a+2)}$,1+a+$\sqrt{a(a+2)}$).
点评 本题考查不等式的解法和运用,注意方程和不等式的关系,运用分类讨论的思想方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.正四面体ABCD中,M,N分别是棱BC和棱AC的中点,则异面直线AM和DN所成的角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 0 |
12.设F1、F2分别是椭圆$\frac{x^2}{4}$+y2=1的左、右焦点,若Q是该椭圆上的一个动点,则$\overrightarrow{Q{F_1}}$•$\overrightarrow{Q{F_2}}$的最大值和最小值分别为( )
| A. | 1与-2 | B. | 2与-2 | C. | 1与-1 | D. | 2与-1 |
9.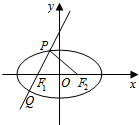 已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
 已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
10.一个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 6π | B. | 7π | C. | 8π | D. | 9π |