题目内容
11.已知偶函数f(x)在区间(0,+∞)单调增加,则满足f(x-1)<f($\frac{1}{3}$)的x取值范围是( )| A. | (-$\frac{1}{3}$,$\frac{1}{3}$) | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | ($\frac{2}{3}$,$\frac{4}{3}$) | D. | [$\frac{2}{3}$,$\frac{4}{3}$] |
分析 根据函数的奇偶性和单调性之间的关系,将不等式进行转化,即可得到不等式的解集.
解答 解:∵偶函数f(x)在[0,+∞)上为增函数,
∴不等式f(x-1)<f($\frac{1}{3}$)等价为f(|x-1|)<f($\frac{1}{3}$),
即|x-1|<$\frac{1}{3}$,
即-$\frac{1}{3}$<x-1<$\frac{1}{3}$,
即$\frac{2}{3}$<x<$\frac{4}{3}$,
故不等式的解集为($\frac{2}{3}$,$\frac{4}{3}$),
故选:C.
点评 本题主要考查不等式的解法,利用函数的奇偶性和单调性之间的关系是解决本题的关键,综合考查函数性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知函数y=f(x)是定义域为R的奇函数.当x≥0时f(x)=$\left\{{\begin{array}{l}{{x^2},0≤x≤1}\\{f(x-1)+1,x>1}\end{array}}\right.$.若恰有5个不同的实数x1,x2,…,x5,使得f(x)=mx成立,则实数m的值为( )
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | 3-2$\sqrt{2}$ |
9.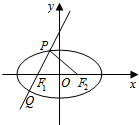 已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
 已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |