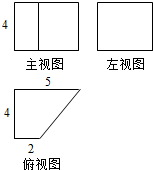
题目内容

12．已知△ABC的三个内角满足sinA=sinBcosC，则△ABC的形状一定是直角三角形．

分析 利用两角和差的正弦公式将条件进行化简即可得到结论．

解答 解：由sinA=sinBcosC得sin（B+C）=sinBcosC，
即sinBcosC+cosBsinC=sinBcosC，
即cosBsinC=0，
在三角形中，cosB≠0，
则有sinC=0，即C=90°，
即三角形为直角三角形，
故答案为：直角三角形

点评 本题主要考查三角形形状的判断，利用两角和差的正弦公式进行化简是解决本题的关键．

练习册系列答案
相关题目
2．若椭圆经过原点，且焦点为F1（-1，0）、F2（-3，0），则其离心率为（　　）
A．$\frac{1}{4}$B．$\frac{1}{2}$C．$\frac{2}{3}$D．$\frac{3}{4}$
3．设a＞0，b＞0，若3是9a与27b的等比中项，则$\frac{3}{a}$+$\frac{2}{b}$的最小值为（　　）
A．25B．24C．36D．12
20．某几何体的三视图如图所示，则该几何体的表面积是92
7．已知△ABC的三个内角A，B，C所对的边分别为a，b，c，向量$\overrightarrow m$=（a+b，a-c），$\overrightarrow n$=（sinC，sinA-sinB），且$\overrightarrow m$∥$\overrightarrow n$．
（1）求∠B的大小．
（2）若a=1，b=$\sqrt{3}$，求△ABC的面积．
17．图中所示算法流程图的功能是（　　）
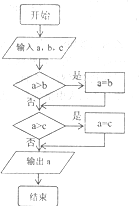
A．求a、b、c三数的最大数B．求a、b、c三数的最小数
C．将a、b、c三数由大到小排列D．将a、b、c三数由小到大排列
4．已知解集A={y|y=2n（n∈N*）}，B={y|y=2n+1，n∈N*}，则A∩B中有（　　）个元素．
A．0B．1C．2D．3
1．定义在区间I上的函数f（x），若任给x0∈I，均有f（x0）∈I，则称函数f（x）在区间I上“定义域与值域的包含”
（1）已知函数f（x）=2x+1；g（x）=-$\frac{3}{4}$x2+$\frac{3}{2}$x+$\frac{5}{4}$判断函数f（x）、g（x）在区间[-1，2]是否“定义域与值域的包含“，并说明理由；
（2）函数h（x）=$\frac{2x+m}{x+2}$在区间[2，8]上“定义域与值域的包含”，求实数m的取值范围．
2．已知$\overrightarrow{a}$=（cosωx，sinωx），$\overrightarrow{b}$=（cosωx，-$\sqrt{3}$cosωx），函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$-$\frac{1}{2}$，若直线x=$\frac{π}{3}$是y=f（x）图象的一条对称轴．
（1）求正数ω的最小值；
（2）当正数ω取最小值时，求函数f（x）的单调区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网