题目内容
10.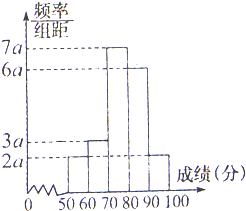 200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示:
200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示:(Ⅰ)求频率分布直方图中a的值;
(Ⅱ) 分别求出成绩落在区间[50,60)与区间[60,70)中的学生人数;
(Ⅲ)现用分层抽样的方法从这200名学生中抽取20人进行成绩分析,试求成绩在区间[80,90)中抽样学生的人数.
分析 (Ⅰ)根据频率和为1,列出方程,求出a的值;
(Ⅱ)根据频率=$\frac{频数}{样本容量}$,求出对应的频数即可;
(Ⅲ)根据分层抽样原理,计算成绩在区间[80,90)中应抽取的人数.
解答 解:(Ⅰ)根据频率和为1,得;
(2a+3a+7a+6a+2a)×10=1,
解得a=0.005;
(Ⅱ)成绩落在区间[50,60)内的频率是:10×2a=20×0.005=0.1,
∴该区间内的学生数是:200×0.1=20;
成绩在区间[60,70)内的频率是:10×3a=30×0.005=0.15,
∴该区间内的学生数是:200×0.15=30;
(Ⅲ)用分层抽样方法从这200名学生中抽取20人,
成绩在区间[80,90)中应抽取的学生人数为:
20×$\frac{6a}{2a+3a+7a+6a+2a}$=6.
点评 本题考查了频率分布直方图的应用问题,也考查了分层抽样方法的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.在△ABC中,若∠A=60°,∠B=45°,BC=3$\sqrt{2}$,则AC等于( )
| A. | 4$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
5.执行如图所示的程序框图,若输入的x为2,则输出的x为( )


| A. | 11 | B. | 23 | C. | 30 | D. | 47 |
15.△ABC外接圆的圆心O,半径为1,若$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AO}$,且|$\overrightarrow{AC}$|=|$\overrightarrow{AO}$|,则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{3}{2}$ |