题目内容
17.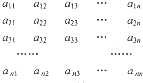 如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )
如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )| A. | $\frac{1031}{512}$ | B. | $\frac{1031}{512}$ | C. | $\frac{1013}{1024}$ | D. | $\frac{1031}{1024}$ |
分析 根据等比数列、等差数列的定义求得q,进而可知ann=$\frac{n}{2}×(\frac{1}{2})^{n-1}$=$\frac{n}{{2}^{n}}$,进而根据错位相减法求得结论.
解答 解:设公比为q,因为a11=a22=a34=$\frac{1}{2}$,所以a21=$\frac{1}{2}$q,a31=$\frac{1}{2}$q2,a32=$\frac{1}{2}$q.
由a31,a32,a33,a34成等差数列,有a34=a31+3(a32-a31),得q=1(舍)或q=$\frac{1}{2}$.
所以a12=1,a1n=$\frac{n}{2}$,ann=$\frac{n}{2}×(\frac{1}{2})^{n-1}$=$\frac{n}{{2}^{n}}$,
所以a11+a22+a33+…+a99=$\frac{1}{2}$+$\frac{2}{{2}^{2}}$+…+$\frac{9}{{2}^{9}}$,
由错位相减法可得a11+a22+a33+…+a99=$\frac{1013}{512}$.
故选:B.
点评 本题主要考查等差数列、等比数列的性质,考查错位相减法,考查了学生综合分析问题的能力.

练习册系列答案
相关题目
8.已知函数f(x)=sin4x-cos4x,则f(x)的最小正周期是( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
5.执行如图所示的程序框图,若输入的x为2,则输出的x为( )


| A. | 11 | B. | 23 | C. | 30 | D. | 47 |