题目内容
20．某几何体的三视图如图所示，则该几何体的表面积是92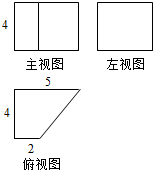
分析 根据几何体的三视图，得出该几何体是底面为直角梯形的四棱柱，根据图中数据求出它的表面积．
解答 解：根据几何体的三视图，得；
该几何体是底面为直角梯形的直四棱柱，
且直四棱柱的高为4，底面直角梯形的上底边长为2，下底边长为5，高为4；
所以该四棱柱的表面积为
S=2×$\frac{1}{2}$×（2+5）×4+（2+4+5+$\sqrt{{3}^{2}{+4}^{2}}$）×4=92．
故答案为：92．
点评 本题考查了空间几何体的三视图的应用问题，解题的关键是根据三视图得出几何体的形状特征，是基础题目．
练习册系列答案
相关题目
10．曲线$\frac{x^2}{25}+\frac{y^2}{5}$=1与曲线$\frac{x^2}{n}+\frac{y^2}{5n}$=1（n＞0）有相同的（ ）
| A． | 焦点 | B． | 焦距 | C． | 离心率 | D． | 准线 |
5．定积分$\int_0^1{（2x-{e^x}）}$dx的值为（ ）
| A． | 2-e | B． | -e | C． | e | D． | 2+e |
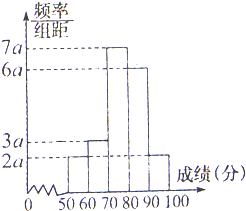200名学生，某次数学考试成绩（单位：分）的频率分布直方图如图所示：