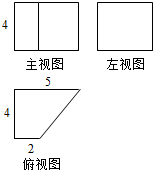
题目内容
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为2,它的一个焦点与抛物线y2=8x的焦点相同,那么双曲线的渐近线方程为$y=±\sqrt{3}x$.分析 先根据抛物线y2=8x的方程求出焦点坐标,得到双曲线的c值,再由离心率求出a的值,得到b的值,可得到双曲线的渐近线的方程.
解答 解:∵抛物线y2=8x的焦点为(2,0),
曲线的焦点坐标为:(2,0),(-2,0);
故双曲线中的c=2,且满足$\frac{c}{a}$=2,故a=1,b=$\sqrt{3}$,
所以双曲线的渐近线方程为$y=±\sqrt{3}x$.
故答案为:$y=±\sqrt{3}x$.
点评 本题主要考查圆锥曲线的基本元素之间的关系问题,同时双曲线、椭圆的相应知识也进行了综合性考查.

练习册系列答案
相关题目
2.若椭圆经过原点,且焦点为F1(-1,0)、F2(-3,0),则其离心率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
6.设函数y=sin2x+$\sqrt{3}$cos2x的最小正周期为T,最大值为A,则( )
| A. | T=2π,A=2 | B. | T=2π,A=$\sqrt{2}$ | C. | T=π,A=2 | D. | T=π,A=$\sqrt{2}$ |
3.设a>0,b>0,若3是9a与27b的等比中项,则$\frac{3}{a}$+$\frac{2}{b}$的最小值为( )
| A. | 25 | B. | 24 | C. | 36 | D. | 12 |