题目内容
14. 一座圆形拱桥,当水面在如图所示位置时,拱桥离水面2米,水面宽12米,当水面下降1米后水面宽为2$\sqrt{51}$米.
一座圆形拱桥,当水面在如图所示位置时,拱桥离水面2米,水面宽12米,当水面下降1米后水面宽为2$\sqrt{51}$米.
分析 先根据题目条件建立适当的直角坐标系,得到各点的坐标,通过设圆的半径,可得圆的方程,然后将点的坐标代入确定圆的方程,设当水面下降1米后可设A′的坐标为(x0,-3)(x0>0)根据点在圆上,可求得x0的值,从而得到问题的结果.
解答 解:以圆拱拱顶为坐标原点,以过拱顶顶点的竖直直线为y轴,建立直角坐标系,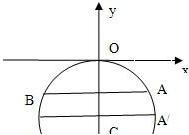 设圆心为C,水面所在弦的端点为A,B,则由已知可得:A(6,-2),
设圆心为C,水面所在弦的端点为A,B,则由已知可得:A(6,-2),
设圆的半径为r,则C(0,-r),即圆的方程为x2+(y+r)2=r2,
将A的坐标代入圆的方程可得r=10,
所以圆的方程是:x2+(y+10)2=100
则当水面下降1米后可设A′的坐标为(x0,-3)(x0>0)
代入圆的方程可得x0=$\sqrt{51}$,
所以当水面下降1米后,水面宽为2$\sqrt{51}$米.
故答案为:2$\sqrt{51}$.
点评 本题考查了圆的方程的综合应用,以及点在圆上的条件的转化,圆的对称性的体现,是个基础题.

练习册系列答案
相关题目
4.如果满足9x-a≥0>8x-b的实数x的整数值只有1,2,3,那么满足这个条件的整式a,b的有序实数对(a,b)共有( )
| A. | 48对 | B. | 63对 | C. | 64对 | D. | 72对 |
5.已知某个车轮旋转的角度α(弧度)与时间t(秒)的函数关系是α=$\frac{2π}{0.64}$t2(t≥0),则车轮启动后第1.6秒时的瞬时角速度是( )
| A. | 20π弧度/秒 | B. | 10π弧度/秒 | C. | 8π弧度/秒 | D. | 5π弧度/秒 |
2.若点(-2,-1)是圆(x+1)2+y2=1的弦AB的中点,则直线AB的方程为( )
| A. | x-y+1=0 | B. | 3x+y+7=0 | C. | x+y+3=0 | D. | x-3y-1=0 |
9.已知直线l经过点A(4,1),B(6,3),则直线l的倾斜角是( )
| A. | 0° | B. | 30° | C. | 45° | D. | 60° |