题目内容
11.已知函数f(x)=$\frac{1}{3}{x^3}+a{x^2}+{b^2}$x,若a是从1,2,3三个数中任取的一个数,b是从0,1,2三个数中任取的一个数,则使函数f(x)有极值点的概率为$\frac{2}{3}$.分析 根据f(x)有极值,得到f'(x)=0有两个不同的根,求出a,b的关系,根据古典概型求出概率即可.
解答 解:∵函数f(x)=$\frac{1}{3}{x^3}+a{x^2}+{b^2}$x有两个极值点,
∴f′(x)=x2+2ax+b2有两个不同的根,
即判别式△=4a2-4b2>0,
即当a>b,该函数有两个极值点,
a从1,2,3三个数中任取的一个数,b是从0,1,2三个数中任取的一个数的基本事件有9种,
满足a>b的基本事件有(1,0),(2,0),(2,1),(3,0),(3,1),(3,2)共6种,
故函数有两个极值点的概率为P=$\frac{6}{9}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题主要考查古典概型的概率的计算,利用函数取得极值的条件求出对应a,b的关系是解决本题的关键.

练习册系列答案
相关题目
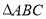 中,角
中,角 所对的边分别为
所对的边分别为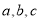 ,且
,且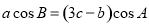 .
. ,求
,求 ;
; ,且
,且 的面积为
的面积为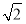 ,求
,求 的周长.
的周长.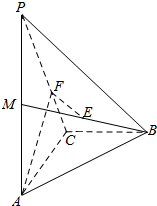 如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.
如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.