题目内容
14.在平面直角坐标系中,以原点为极点,x轴非负半轴为极轴极坐标,曲线C1的方程:$\left\{\begin{array}{l}{x=\sqrt{2}+cosα}\\{y=\sqrt{2}+sinα}\end{array}\right.$(α为参数),曲线C2的方程:$ρ=\frac{8}{sin(θ+\frac{π}{4})}$.(1)求曲线C1和曲线C2的直角坐标系方程;
(2)从C2上任意一点P作曲线C1的切线,设切点为Q,求切线长PQ的最小值及此时点P的极坐标.
分析 (I)利用sin2α+cos2α=1可把曲线曲线C1的方程:$\left\{\begin{array}{l}{x=\sqrt{2}+cosα}\\{y=\sqrt{2}+sinα}\end{array}\right.$(α为参数),化为直角坐标方程.由曲线C2的方程:$ρ=\frac{8}{sin(θ+\frac{π}{4})}$.展开化为$\frac{\sqrt{2}}{2}(ρcosθ+ρsinθ)=8$,代入$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,即可化为直角坐标方程.
(II)根据题意设曲线C1的圆心为M,则|PQ|=$\sqrt{|PM{|}^{2}-1}$,当|PQ|最短时,|PM|最小,当PM⊥C2时,|PM|最短,利用点到直线的距离公式距离可得|PM|,即可得出.
解答 解:(I)曲线C1的方程:$\left\{\begin{array}{l}{x=\sqrt{2}+cosα}\\{y=\sqrt{2}+sinα}\end{array}\right.$(α为参数),可得$(x-\sqrt{2})^{2}+(y-\sqrt{2})^{2}=1$.
由曲线C2的方程:$ρ=\frac{8}{sin(θ+\frac{π}{4})}$.展开化为$\frac{\sqrt{2}}{2}(ρcosθ+ρsinθ)=8$,化为x+y-8$\sqrt{2}$=0.
(II)根据题意设曲线C1的圆心为M,则|PQ|=$\sqrt{|PM{|}^{2}-1}$,当|PQ|最短时,|PM|最小,
当PM⊥C2时,|PM|最短,此时|PM|=$\frac{|\sqrt{2}+\sqrt{2}-8\sqrt{2}|}{\sqrt{2}}$=6,
此时PM的直线方程为y=x,可得P$(4\sqrt{2},4\sqrt{2})$.
化为极坐标P$(8,\frac{π}{4})$,|PQ|的最小值=$\sqrt{{6}^{2}-1}$=$\sqrt{35}$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、点到直线的距离公式、勾股定理,考查了推理能力与计算能力,属于中档题.

 走进文言文系列答案
走进文言文系列答案| A. | (0,1) | B. | (0,2) | C. | (1,+∞) | D. | (2,+∞) |
| PM 2.5日均值(微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM 2.5监测数据超标的天数,求ξ的分布列;
(3)以这10天的PM 2.5日均值来估计一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级(精确到整数).
 ________.
________.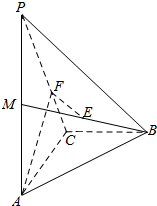 如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.
如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.