题目内容
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0),且椭圆上的点到一个焦点的最短距离为
=1(a>b>0),且椭圆上的点到一个焦点的最短距离为![]() b.
b.
(1)求椭圆C的离心率;
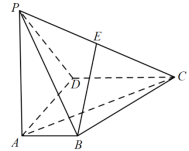
(2)若点M(![]() ,
,![]() )在椭圆C上,不过原点O的直线l与椭圆C相交于A,B两点,与直线OM相交于点N,且N是线段AB的中点,求△OAB面积的最大值.
)在椭圆C上,不过原点O的直线l与椭圆C相交于A,B两点,与直线OM相交于点N,且N是线段AB的中点,求△OAB面积的最大值.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)由题意,得![]() ,然后求解离心率即可;
,然后求解离心率即可;
(2)由(1)得a=2c,则b2=3c2.将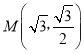 代入椭圆方程可解得c=1,求出椭圆方程,直线OM的方程为
代入椭圆方程可解得c=1,求出椭圆方程,直线OM的方程为![]() ,当直线l的斜率不存在时,AB的中点不在直线
,当直线l的斜率不存在时,AB的中点不在直线![]() 上,故直线l的斜率存在.设直线l的方程为y=kx+m(m≠0),与椭圆联立消y,设A,B坐标,利用韦达定理求出AB的中点
上,故直线l的斜率存在.设直线l的方程为y=kx+m(m≠0),与椭圆联立消y,设A,B坐标,利用韦达定理求出AB的中点![]() ,代入可得k值,再利用判别式推出
,代入可得k值,再利用判别式推出![]() ,且m≠0,利用弦长公式以及三角形的面积,利用均值不等式可得最值.
,且m≠0,利用弦长公式以及三角形的面积,利用均值不等式可得最值.
(1)由题意,得![]() ,
,
则![]() ,结合b2=a2-c2,得
,结合b2=a2-c2,得![]() ,
,
即2c2-3ac+a2=0,
亦即2e2-3e+1=0,结合0<e<1,解得![]() ,
,
所以椭圆C的离心率为![]() .
.
(2)由(1)得a=2c,则b2=3c2,
将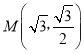 代入椭圆方程
代入椭圆方程![]() ,解得c=1,
,解得c=1,
所以椭圆方程为![]() ,
,
易得直线OM的方程为![]() ,
,
当直线l的斜率不存在时,AB的中点不在直线![]() 上,故直线l的斜率存在,
上,故直线l的斜率存在,
设直线l的方程为y=kx+m(m≠0),与![]() 联立,
联立,
消y得(3+4k2)x2+8kmx+4m2-12=0,
所以![]() =64k2m2-4(3+4k2)(4m2-12)
=64k2m2-4(3+4k2)(4m2-12)
=48(3+4k2-m2)>0.
设A(x1,y1),B(x2,y2),
则![]() ,
,![]() ,
,
由![]() ,
,
得AB的中点![]() ,
,
因为N在直线![]() 上,
上,
所以![]() ,解得k=-
,解得k=-![]() .
.
所以![]() =48(12-m2)>0,得-
=48(12-m2)>0,得-![]() ,且m≠0,
,且m≠0,
|AB|=![]() |x2-x1|
|x2-x1|
=![]()
=![]()
=![]() .
.
又原点O到直线l的距离d=![]() ,
,
所以![]()
![]()
![]() ,
,
当且仅当12-m2=m2,m=![]() 时等号成立,符合-
时等号成立,符合-![]() ,且m≠0,
,且m≠0,
所以△OAB面积的最大值为:![]() .
.

 津桥教育计算小状元系列答案
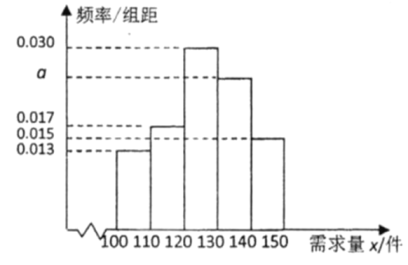
津桥教育计算小状元系列答案【题目】某超市试销某种商品一个月,获得如下数据:
日销售量(件) |
|
|
|
|
|
频率 |
|
|
|
|
|
试销结束后(假设该商品的日销售量的分布规律不变),超市决定正式营销这种商品.设某天超市开始营业时有该商品![]() 件,当天营业结束后检查存货,若发现存货少于
件,当天营业结束后检查存货,若发现存货少于![]() 件,则当天进货补充至
件,则当天进货补充至![]() 件,否则不进货.将频率视为概率.
件,否则不进货.将频率视为概率.
![]() 求当天商品进货的概率.
求当天商品进货的概率.
![]() 记
记![]() 为第二天开始营业时该商品的件数.
为第二天开始营业时该商品的件数.
![]() 求
求![]() 得分布列.
得分布列.
![]() 求
求![]() 得数学期望与方差.
得数学期望与方差.
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?参考公式: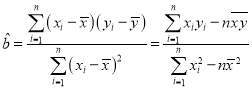 ,
,![]() .
.