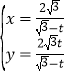题目内容
【题目】抛物线C的顶点在坐标原点,对称轴为x轴,抛物线C过点A(4,4),过抛物线C的焦点F作倾斜角等于45°的直线l,直线l交抛物线C于M、N两点.
(1)求抛物线C的方程;
(2)求线段MN的长.
【答案】(1)y2=4x;(2)8
【解析】
(1)设出直线方程,代入点的坐标可得抛物线方程;
(2)写出直线方程,和抛物线联立,结合韦达定理和抛物线定义可得弦长.
(1)依题意设抛物线C的方程为y2=2px,将A(4,4)代入得p=2,所以抛物线C的方程为y2=4x.
(2)F(1,0),直线l:y=x﹣1,联立![]() 得x2﹣6x+1=0,
得x2﹣6x+1=0,
设A(x1,y1),B(x2,y2),则x1+x2=6,根据抛物线的定义可得|MN|=x1+x2+p=6+2=8.

练习册系列答案
相关题目
【题目】抽样得到某次考试中高二年级某班![]() 名学生的数学成绩和物理成绩如下表:
名学生的数学成绩和物理成绩如下表:
学生编号 |
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
物里成绩 |
|
|
|
|
|
|
(1)在图中画出表中数据的散点图;
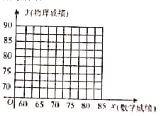
(2)建立![]() 关于
关于![]() 的回归方程:(系数保留到小数点后两位).
的回归方程:(系数保留到小数点后两位).
(3)如果某学生的数学成绩为![]() 分,预测他本次的物理成绩(成绩取整数).
分,预测他本次的物理成绩(成绩取整数).
参考公式:回归方程为![]() ,其中
,其中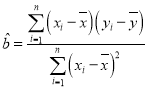 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.