题目内容
13.如图1,在四棱锥P-ABCD中PD⊥底面ABCD,底面ABCD是直角梯形,M为侧棱PD上一点.该四棱锥的俯视图与侧(左)视图如图2所示.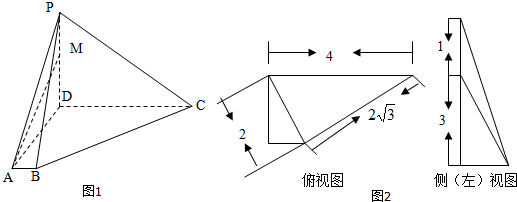
(Ⅰ)证明:BC⊥平面PBD;
(Ⅱ)证明:AM∥平面PBC;
(Ⅲ)求四棱锥P-ABCD的体积.
分析 (Ⅰ)利用俯视图和勾股定理的逆定理可得BC⊥BD,利用线面垂直的性质定理可得BC⊥PD,再利用线面垂直的判定定理即可证明;
(Ⅱ)取PC上一点Q,使PQ:PC=1:4,连接MQ,BQ.利用左视图和平行线分线段成比例的判定和性质即可得出MQ∥CD,MQ=$\frac{1}{4}$CD.
再利用平行四边形的判定和性质定理即可得出AM∥BQ,利用线面平行的判定定理即可证明.
(Ⅲ)利用棱锥的体积公式,即可求四棱锥P-ABCD的体积.
解答 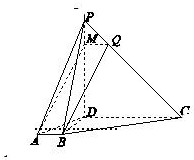 (Ⅰ)证明:由俯视图可得,BD2+BC2=CD2,
(Ⅰ)证明:由俯视图可得,BD2+BC2=CD2,
∴BC⊥BD.
又∵PD⊥平面ABCD,
∴BC⊥PD,
又∵BD∩PD=D,
∴BC⊥平面PBD.
(Ⅱ)证明:取PC上一点Q,使PQ:PC=1:4,连接MQ,BQ.
由左视图知 PM:PD=1:4,∴MQ∥CD,MQ=$\frac{1}{4}$CD.
在△BCD中,易得∠CDB=60°,∴∠ADB=30°.
又 BD=2,∴AB=1,AD=$\sqrt{3}$.
又∵AB∥CD,AB=$\frac{1}{4}$CD,
∴AB∥MQ,AB=MQ.
∴四边形ABQM为平行四边形,
∴AM∥BQ.
∵AM?平面PBC,BQ?平面PBC,
∴直线AM∥平面PBC.
(Ⅲ)解:∵底面ABCD是直角梯形,AD⊥CD,AD⊥AB,AB=1,CD=4,AD=$\sqrt{3}$,
∴SABCD=$\frac{1}{2}•(1+4)•\sqrt{3}$,
∵PD⊥底面ABCD,PD=4,
∴V=$\frac{1}{3}$•SABCD•PD=$\frac{1}{3}•\frac{1}{2}•(1+4)•\sqrt{3}•4$=$\frac{10\sqrt{3}}{3}$.
点评 熟练掌握由三视图得到线面位置关系和数据、线面垂直的判定和性质定理、线面平行的判定和性质定理、求四棱锥P-ABCD的体积是解题的关键.

| A. | 2012 | B. | 4024 | C. | 2014 | D. | 4025 |
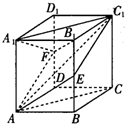 如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.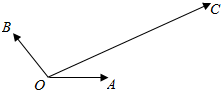 如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=2$\sqrt{3}$,用$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$为$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$.
如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=2$\sqrt{3}$,用$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$为$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$.