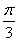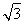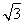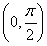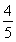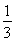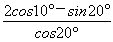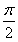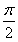题目内容
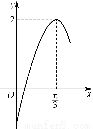
已知a>0,函数f(x)=-2asin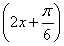 +2a+b,当x∈
+2a+b,当x∈ 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.
(1)求常数a、b的值;
(2)设g(x)=f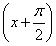 且lgg(x)>0,求g(x)的单调区间.
且lgg(x)>0,求g(x)的单调区间.
(1)a=2,b=-5.(2)单调增区间为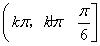 (k∈Z),单调减区间为
(k∈Z),单调减区间为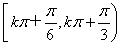 (k∈Z)
(k∈Z)
【解析】(1)∵x∈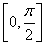 ,∴2x+
,∴2x+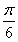 ∈
∈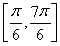 .∴sin
.∴sin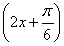 ∈
∈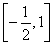 ,
,
∴-2asin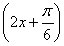 ∈[-2a,a],∴f(x)∈[b,3a+b].
∈[-2a,a],∴f(x)∈[b,3a+b].
又∵-5≤f(x)≤1,∴b=-5,3a+b=1,因此a=2,b=-5.
(2)由(1)知a=2,b=-5,∴f(x)=-4sin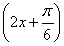 -1,
-1,
g(x)=f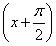 =-4sin
=-4sin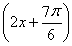 -1=4sin
-1=4sin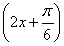 -1.
-1.
又由lgg(x)>0,得g(x)>1,∴4sin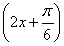 -1>1,∴sin
-1>1,∴sin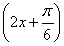 >
>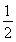 ,
,
∴2kπ+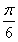 <2x+
<2x+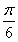 <2kπ+
<2kπ+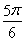 ,k∈Z.
,k∈Z.
由2kπ+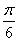 <2x+
<2x+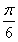 ≤2kπ+
≤2kπ+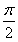 (k∈Z),得g(x)的单调增区间为
(k∈Z),得g(x)的单调增区间为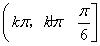 (k∈Z).
(k∈Z).
由2kπ+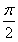 ≤2x+
≤2x+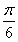 <2kπ+
<2kπ+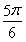 ,得g(x)的单调减区间为
,得g(x)的单调减区间为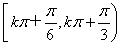 (k∈Z)
(k∈Z)

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目