题目内容
15.已知数列{an}是等差数列,其前n项和为Sn,首项a1=-2015且$\frac{{S}_{2014}}{2014}$-$\frac{{S}_{2012}}{2012}$=2,则S2015=-2015.分析 根据等差数列前n项和公式化简已知的式子求出公差d的值,代入S2015化简求值.
解答 解:设等差数列{an}的公差为d,
∵$\frac{{S}_{2014}}{2014}$-$\frac{{S}_{2012}}{2012}$=2,
∴$\frac{2014{a}_{1}+\frac{2014×2013}{2}d}{2014}$-$\frac{2012{a}_{1}+\frac{2012×2011}{2}d}{2}$=2,
即$\frac{2013}{2}$d-$\frac{2011}{2}$d=2,
即d=2,
又a1=-2015,
∴S2015=$2015{a}_{1}+\frac{2015×2014}{2}×d$=2015(a1+2014)=2015(-2015+2014)=-2015,
故答案为:-2015.
点评 本题考查等差数列前n项和公式的应用,以及化简、计算能力,属于中档题.

练习册系列答案
相关题目
6.函数f(x)=-x3+ax在[0,+∞)上是减函数,则a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,+∞) | D. | [0,+∞) |
10.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是( )
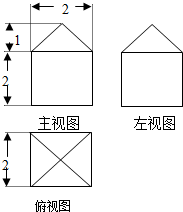

| A. | $(20+4\sqrt{3})c{m^2}$ | B. | $(20+4\sqrt{2})c{m^2}$ | C. | $(20+\sqrt{2})c{m^2}$ | D. | $(10+4\sqrt{2})c{m^2}$ |
4.函数f(x)=sinx-2x在区间[0,2π]上的最小值是( )
| A. | -4π | B. | 0 | C. | -2π | D. | 1-π |
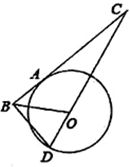 已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.
已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$. 如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.
如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.