题目内容
(本小题满分12分)已知数列{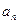 }满足
}满足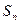 =
=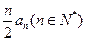 ,
,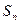 是{
是{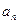 }的前
}的前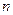 项的和,
项的和,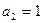 . (1)求
. (1)求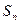 ;(2)证明:
;(2)证明: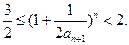
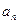 }满足
}满足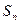 =
=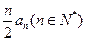 ,
,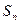 是{
是{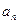 }的前
}的前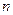 项的和,
项的和,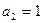 . (1)求
. (1)求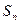 ;(2)证明:
;(2)证明: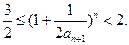
(1)Sn=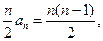 (2)略
(2)略
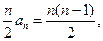 (2)略
(2)略(1)由题意Sn=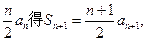
两式相减得2an+1=(n+1)an+1-nan即(n-1)an+1=nan,
所以 再相加得
再相加得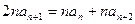 即
即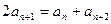
所以数列{an}是等差数列. ………………4分
∵a1=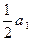 ∴a1=0,
∴a1=0,
又a2=1,则公差为1,∴an=n-1,
所以数列{an}的前n项的和为Sn=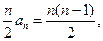 ………………6分
………………6分
(2)(1+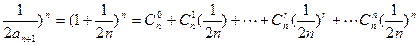
………………8分
①当n=1时:(1+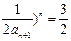
②当n≥2时:
∵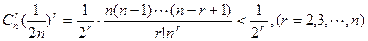 ………………10分
………………10分
∴(1+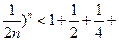 …+
…+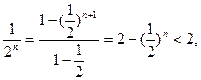
而(1+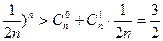 ,∴
,∴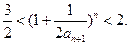
综上所证: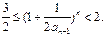 ………………12分
………………12分
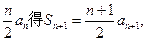
两式相减得2an+1=(n+1)an+1-nan即(n-1)an+1=nan,
所以
 再相加得
再相加得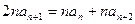 即
即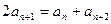
所以数列{an}是等差数列. ………………4分
∵a1=
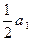 ∴a1=0,
∴a1=0,又a2=1,则公差为1,∴an=n-1,
所以数列{an}的前n项的和为Sn=
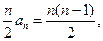 ………………6分
………………6分(2)(1+
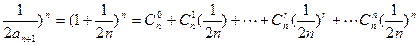
………………8分
①当n=1时:(1+
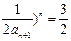
②当n≥2时:
∵
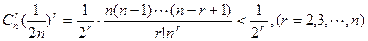 ………………10分
………………10分∴(1+
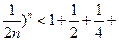 …+
…+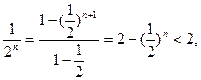
而(1+
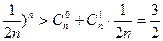 ,∴
,∴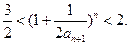
综上所证:
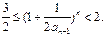 ………………12分
………………12分
练习册系列答案
相关题目
 ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 ,求数列{cn}的前n项的和Tn;
,求数列{cn}的前n项的和Tn; 的最大值.
的最大值.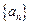 满足
满足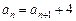 ,
,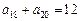 ,等比数列
,等比数列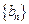 的首项为2,公比为
的首项为2,公比为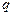 。
。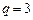 ,问
,问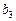 等于数列
等于数列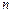 项和分别记为
项和分别记为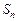 和
和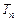 ,
,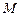 ,当
,当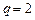 时,试比较
时,试比较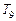 的大小
的大小
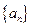 的前
的前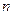 项和为
项和为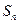 且满足:
且满足: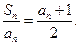
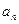 ;(Ⅱ)若
;(Ⅱ)若 求证:
求证: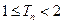
 满足:
满足: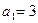 ,且
,且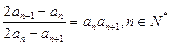 .
.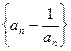 是等比数列;
是等比数列;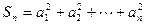 ,
,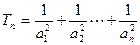 ,求
,求 ,并确定最小的正整数n,使
,并确定最小的正整数n,使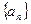 中,
中,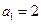 ,
,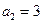 ,其前
,其前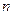 项和
项和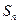 满足
满足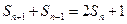 其中(
其中(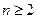 ,
,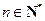 ).
).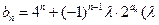 为非零整数,
为非零整数,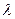 的值,使得对任意
的值,使得对任意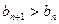 成立.
成立.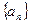 ,
,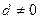 ,
,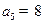 ,且项
,且项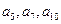 分别是某一等比数列
分别是某一等比数列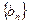 中的第
中的第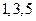 项,(1)求数列
项,(1)求数列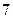 项。
项。 中,
中, ,前4项和为1111,则该数列的公比为( )
,前4项和为1111,则该数列的公比为( )
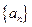 中,
中,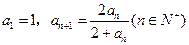 ,则
,则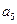 等于______ _.
等于______ _.