题目内容
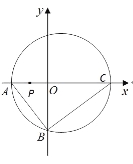
【题目】已知椭圆
的中心在原点
，焦点在
轴上，离心率为
，右焦点到右顶点的距离为
．
（1）求椭圆的标准方程；
（2）是否存在与椭圆交于
两点的直线
，使得
成立？若存在，求出实数
的取值范围，若不存在，请说明理由．
【答案】（1）
；（2）存在，
．
【解析】试题分析：（1）由已知条件推导出
，
，由此能求出椭圆
的标准方程；（2）直线
与椭圆方程联立方程，得到关于
的一元二次方程，由根的判别式和韦达定理结合已知条件能求出实数
的取值范围．
试题解析：（1）设椭圆的方程为
，半焦距为
．依题意，
由右焦点到右顶点的距离为
，得解得
．所以
，所以椭圆的标准方程是．
（2）解：存在直线，使得
成立．理由如下：
由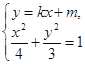
得
．
，化简得
．
设
，则
．
若，所以
，
，
，
，
化简得，
，将
代入中，
，
解得
．又由
，
，
从而，
或
，所以实数的取值范围是
．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
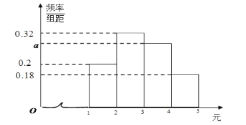
【题目】某班倡议假期每位学生至少阅读一本名著，为了解学生的阅读情况，对该班所有学生进行了调查．调查结果如下表：
阅读名著的本数 | 1 | 2 | 3 | 4 | 5 |
男生人数 | 3 | 1 | 2 | 1 | 3 |
女生人数 | 1 | 3 | 3 | 1 | 2 |
（1）试根据上述数据，求这个班级女生阅读名著的平均本数；
（2）若从阅读
本名著的学生中任选
人交流读书心得，求选到男生和女生各
人的概率；
（3）试比较该班男生阅读名著本数的方差
与女生阅读名著本数的方差
的大小（只需写出结论）．
