题目内容
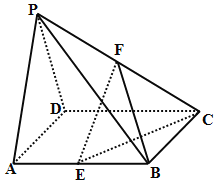
【题目】已知四棱锥![]() ,底面
,底面![]() 是
是![]() ,边长为
,边长为![]() 的菱形,又
的菱形,又![]() 底面
底面![]() ,且
,且![]() ,点
,点![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析: (Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,所以
,所以![]() ,且
,且![]() ,于是
,于是![]() ,由直线与平面平行的判定定理即可证得成立;(Ⅱ)易得
,由直线与平面平行的判定定理即可证得成立;(Ⅱ)易得![]() , 又因为底面
, 又因为底面![]() 是
是![]() 、边长为
、边长为![]() 的菱形,且
的菱形,且![]() 为
为![]() 中点,所以
中点,所以![]() ,由平面与平面垂直的判定定理即可证得.
,由平面与平面垂直的判定定理即可证得.
试题解析:(Ⅰ)证明:取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,
,
因为![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 中点,
中点,
所以![]() ,且
,且![]() ,于是
,于是![]() ,
,
因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,
,
又因为底面![]() 是
是![]() 、边长为
、边长为![]() 的菱形,且
的菱形,且![]() 为
为![]() 中点,
中点,
所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.

点睛:本题给出了特殊的四棱锥,求证线面平行和面面垂直,着重考查了空间平行,垂直的位置关系的判断与证明,属于中档题.线面平行一般利用线线平行推得,即线面平行的判定定理,也可根据面面平行得到;面面垂直的证明主要是利用面面垂直的判定定理证明,或者两个平面所成的二面角的平面角为直角.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目