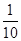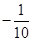题目内容
已知函数f(x)=x3 +x(x∈R).
(1)指出f(x)的奇偶性及单调性,并说明理由;
(2)若a、b、c∈R,且a+b>0,b+c>0,c+a>0,试判断f(a)+f(b)+f(c)的符号.
(1)指出f(x)的奇偶性及单调性,并说明理由;
(2)若a、b、c∈R,且a+b>0,b+c>0,c+a>0,试判断f(a)+f(b)+f(c)的符号.
(1)f(x)为奇函数,且为增函数(2)f(a)+f(b)+f(c)>0.
(1)利用f(-x)与f(x)是相等或相反数,确定是偶函数还是奇函数.
然后利用导数确定其单调性,也可以利用单调性定义进行研究.
(2)把题目条件转化为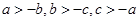 ,再根据f(x)在R上是增函数,所以
,再根据f(x)在R上是增函数,所以
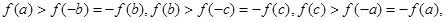 再利用不等式可加性即可得到f(a)+f(b)+f(c)>0
再利用不等式可加性即可得到f(a)+f(b)+f(c)>0
然后利用导数确定其单调性,也可以利用单调性定义进行研究.
(2)把题目条件转化为
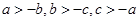 ,再根据f(x)在R上是增函数,所以
,再根据f(x)在R上是增函数,所以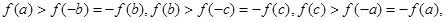 再利用不等式可加性即可得到f(a)+f(b)+f(c)>0
再利用不等式可加性即可得到f(a)+f(b)+f(c)>0
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的最大值是( )
的最大值是( )



 在区间
在区间 上是奇函数,函数
上是奇函数,函数 在区间
在区间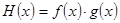 在区间
在区间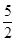 )的值为( )
)的值为( )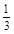
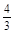
 的导函数是
的导函数是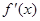 ,且
,且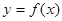 在原点处的切线方程为( )
在原点处的切线方程为( ) 对任意
对任意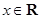 ,都有
,都有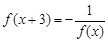 ,且当
,且当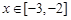 时,
时, ,则
,则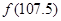 =
=