题目内容
若函数f(x)是定义在R上的偶函数,且对任意x∈R,总有f(x+2)=-f(x)成立,则f(19)等于( )
| A.0 | B.1 | C.18 | D.19 |
A
f(x+2)=-f(x)⇒f(x+4)=-f(x+2)=f(x)⇒周期T=4⇒f(19)=f(-1),
又f(x)是定义在R上的偶函数,得f(-1)=f(1) ①,
且当x=-1时,f(-1+2)=-f(-1),即f(1)=-f(-1) ②,
①②联立得f(-1)=0,所以f(19)=f(-1)=0.
又f(x)是定义在R上的偶函数,得f(-1)=f(1) ①,
且当x=-1时,f(-1+2)=-f(-1),即f(1)=-f(-1) ②,
①②联立得f(-1)=0,所以f(19)=f(-1)=0.

练习册系列答案
相关题目
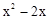 , 当x<0时,f(x)= .
, 当x<0时,f(x)= .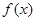 满足:
满足: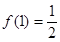 ,
,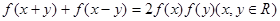 ,则
,则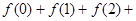 …
…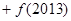 等于( )
等于( )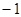
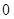
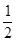
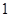
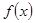 和偶函数
和偶函数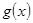 满足
满足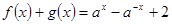
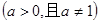 ,
,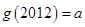 ,则
,则 ( )
( )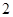
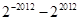
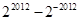
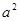
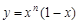 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为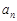 ,则数列
,则数列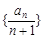 的前n项和的公式是
的前n项和的公式是 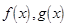 分别为
分别为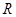 上的奇函数和偶函数,
上的奇函数和偶函数,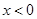 时,
时,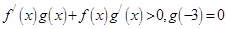 ,则不等式
,则不等式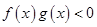 的解集为
的解集为 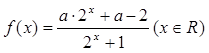 是奇函数,那么a等于
是奇函数,那么a等于 