题目内容
定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
(1)求证:f(0)=1;
(2)求证:对任意的x∈R,恒有f(x)> 0;
(3)证明:f(x)是R上的增函数;(4)若f(x)·f(2x-x2)>1,求x的取值范围。
(1)求证:f(0)=1;
(2)求证:对任意的x∈R,恒有f(x)> 0;
(3)证明:f(x)是R上的增函数;(4)若f(x)·f(2x-x2)>1,求x的取值范围。
(1)略(2)略 (3) 0<x<3
本题主要考查抽象函数及其应用、函数单调性的判断与证明.解本题的关键是灵活应用题目条件,尤其是(3)中“f(x2)=f[(x2-x1)+x1]”是证明单调性的关键,这里体现了向条件化归的策略.
(1)利用赋值法解决,令x=y=0即得;
(2)利用条件:“当x>0时,f(x)>1”,只须证明当x<0时,f(x)>0即可;
(3)利用单调函数的定义证明,设x1<x2,将f(x2)写成f[(x2-x1)+x1]的形式后展开,结合(2)的结论即可证得;
(4)由f(x)•f(2x-x2)>f(0)得f(3x-x2)>f(0).结合f(x)的单调性去掉符号“f”后,转化成一元二次不等式解决即可
(1)利用赋值法解决,令x=y=0即得;
(2)利用条件:“当x>0时,f(x)>1”,只须证明当x<0时,f(x)>0即可;
(3)利用单调函数的定义证明,设x1<x2,将f(x2)写成f[(x2-x1)+x1]的形式后展开,结合(2)的结论即可证得;
(4)由f(x)•f(2x-x2)>f(0)得f(3x-x2)>f(0).结合f(x)的单调性去掉符号“f”后,转化成一元二次不等式解决即可

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
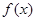 是
是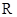 上的奇函数,对
上的奇函数,对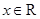 都有
都有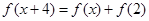 成立,若
成立,若 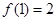 , 则
, 则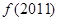 等于( )
等于( )
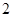
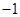
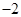
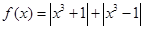 ,则下列坐标表示的点一定在函数f(x)图象上的是( )
,则下列坐标表示的点一定在函数f(x)图象上的是( )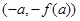
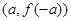
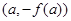
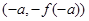
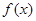 为定义在
为定义在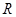 上的奇函数,当
上的奇函数,当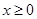 时,
时,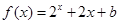 (
(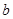 为常数),
为常数), 时,
时,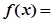
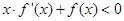 ,则不等式
,则不等式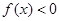 的解集是( )
的解集是( )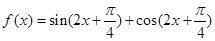 ,则( )
,则( ) 在
在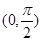 单调递增,其图象关于直线
单调递增,其图象关于直线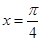 对称
对称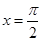 对称
对称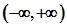 上的偶函数,若对于
上的偶函数,若对于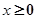 ,都有f(x+2)=f(x),且当
,都有f(x+2)=f(x),且当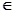 [0,2)时,
[0,2)时,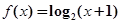 ,则f(-2011)+f(2012) 的值为( )
,则f(-2011)+f(2012) 的值为( )