题目内容
(本小题满分14分)
已知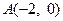 ,
,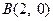 为椭圆
为椭圆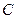 的左、右顶点,
的左、右顶点,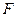 为其右焦点,
为其右焦点,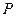 是椭圆
是椭圆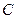 上异于
上异于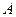 ,
,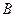 的动点,且
的动点,且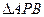 面积的最大值为
面积的最大值为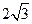 .
.
(Ⅰ)求椭圆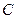 的方程及离心率;
的方程及离心率;
(Ⅱ)直线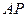 与椭圆在点
与椭圆在点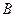 处的切线交于点
处的切线交于点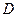 ,当直线
,当直线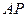 绕点
绕点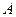 转动时,试判断以
转动时,试判断以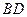

为直径的圆与直线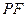 的位置关系,并加以证明.
的位置关系,并加以证明.
已知
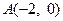 ,
,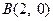 为椭圆
为椭圆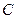 的左、右顶点,
的左、右顶点,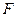 为其右焦点,
为其右焦点,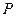 是椭圆
是椭圆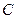 上异于
上异于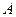 ,
,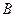 的动点,且
的动点,且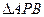 面积的最大值为
面积的最大值为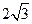 .
. (Ⅰ)求椭圆
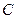 的方程及离心率;
的方程及离心率;(Ⅱ)直线
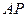 与椭圆在点
与椭圆在点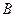 处的切线交于点
处的切线交于点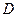 ,当直线
,当直线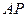 绕点
绕点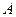 转动时,试判断以
转动时,试判断以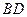

为直径的圆与直线
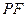 的位置关系,并加以证明.
的位置关系,并加以证明.解:(Ⅰ)由题意可设椭圆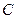 的方程为
的方程为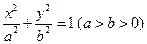 ,
,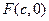 .
.
由题意知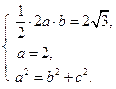 解得
解得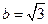
 ,
,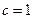 .
.
故椭圆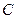 的方程为
的方程为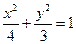 ,离心率为
,离心率为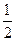 .……6分
.……6分
(Ⅱ)以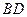 为直径的圆与直线
为直径的圆与直线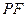 相切.
相切.
证明如下:由题意可设直线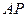 的方程为
的方程为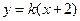
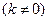 .
.
则点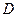 坐标为
坐标为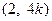 ,
, 中点
中点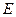 的坐标为
的坐标为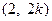 .
.
由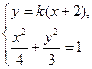 得
得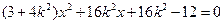 .
.
设点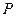 的坐标为
的坐标为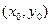 ,则
,则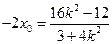 .
.
所以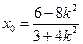 ,
,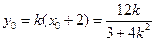 .……………………………10分
.……………………………10分
因为点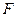 坐标为
坐标为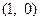 ,
,
当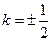 时,点
时,点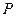 的坐标为
的坐标为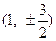 ,点
,点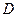 的坐标为
的坐标为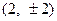 .
.
直线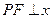 轴,此时以
轴,此时以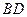 为直径的圆
为直径的圆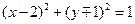 与直线
与直线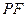 相切
相切 .
.
当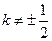 时,则直线
时,则直线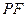 的斜率
的斜率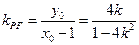 .
.
所以直线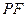 的方程为
的方程为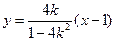 .
.
点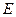 到直线
到直线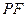 的距离
的距离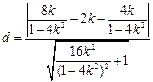
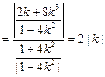 .
.
又因为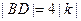 ,所以
,所以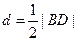 .
.
故以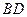 为直径的圆与直线
为直径的圆与直线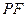 相切.
相切.
综上得,当直线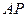 绕点
绕点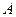
 转动时,以
转动时,以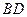 为直径的圆与直线
为直径的圆与直线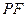 相切.………14分
相切.………14分
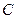 的方程为
的方程为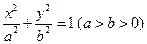 ,
,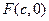 .
.由题意知
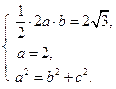 解得
解得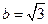
 ,
,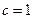 .
. 故椭圆
 的方程为
的方程为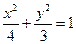 ,离心率为
,离心率为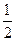 .……6分
.……6分(Ⅱ)以
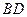 为直径的圆与直线
为直径的圆与直线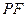 相切.
相切. 证明如下:由题意可设直线
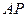 的方程为
的方程为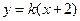
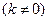 .
.则点
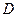 坐标为
坐标为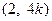 ,
,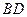 中点
中点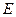 的坐标为
的坐标为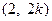 .
.由
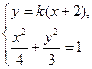 得
得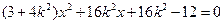 .
.设点
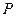 的坐标为
的坐标为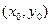 ,则
,则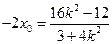 .
.所以
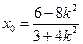 ,
,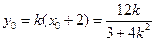 .……………………………10分
.……………………………10分因为点
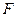 坐标为
坐标为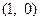 ,
,当
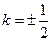 时,点
时,点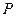 的坐标为
的坐标为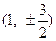 ,点
,点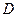 的坐标为
的坐标为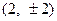 .
.直线
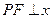 轴,此时以
轴,此时以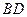 为直径的圆
为直径的圆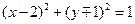 与直线
与直线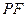 相切
相切 .
.当
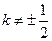 时,则直线
时,则直线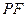 的斜率
的斜率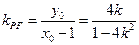 .
.所以直线
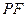 的方程为
的方程为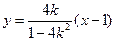 .
.点
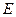 到直线
到直线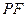 的距离
的距离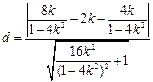
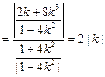 .
.又因为
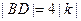 ,所以
,所以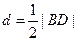 .
.故以
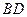 为直径的圆与直线
为直径的圆与直线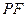 相切.
相切.综上得,当直线
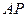 绕点
绕点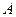
 转动时,以
转动时,以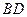 为直径的圆与直线
为直径的圆与直线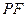 相切.………14分
相切.………14分略

练习册系列答案
相关题目
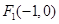 、
、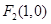 ,且
,且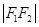 是
是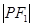 与
与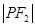 的等差中项,则动点
的等差中项,则动点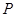 的轨迹方程是( )
的轨迹方程是( )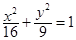
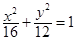
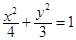
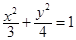
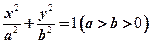 的左、右焦点分别为
的左、右焦点分别为 ,过
,过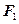 的直线
的直线 与椭圆交于
与椭圆交于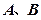 两点。
两点。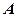 在圆
在圆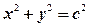 (
(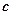 为椭圆的半焦距)上,且
为椭圆的半焦距)上,且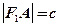 ,求椭圆的离心率;
,求椭圆的离心率; (Ⅱ)若函数
(Ⅱ)若函数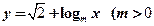 且
且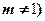 的图象,无论
的图象,无论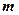 为何值时恒过定点
为何值时恒过定点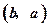 ,求
,求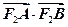 的取值范围。
的取值范围。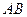 ). 某园林公司承接了该中心花园的施工建设,
). 某园林公司承接了该中心花园的施工建设,
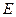 :
: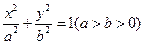 的离心率为
的离心率为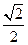 ,且过点
,且过点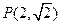 ,设椭圆的右准线
,设椭圆的右准线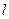 与
与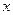 轴的交点为
轴的交点为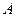 ,椭圆的上顶点为
,椭圆的上顶点为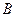 ,直线
,直线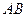 被以原点为圆心的圆
被以原点为圆心的圆 所截得的弦长为
所截得的弦长为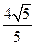 .
.
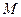 是准线
是准线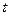 的点,求证:存在一个异于
的点,求证:存在一个异于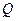 ,对于圆
,对于圆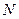 ,有
,有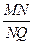 为定值;且当
为定值;且当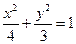 的左、右焦点,曲线C是坐标原点为顶
的左、右焦点,曲线C是坐标原点为顶 点,
点,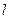 交
交 曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设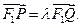
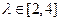 ,求直线
,求直线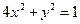 及直线
及直线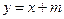 .
.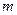 的取值范围.
的取值范围.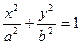
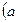 >
>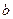 >
>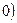 与直线
与直线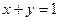 交于
交于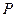 、
、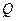 两点,且
两点,且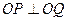 ,其
,其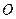 为坐标原点。
为坐标原点。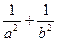 的值;
的值;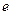 满足
满足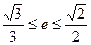 ,求椭圆长轴的取值范围。
,求椭圆长轴的取值范围。 的焦点为F1,F
的焦点为F1,F 2,P为椭圆上一点,若
2,P为椭圆上一点,若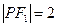 ,则
,则 ( )
( )