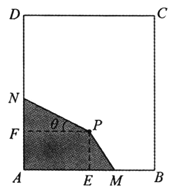
题目内容
【题目】已知双曲线的两个焦点坐标分别为![]() 和
和![]() ,双曲线的一条切线与
,双曲线的一条切线与![]() 轴交于
轴交于![]() ,且斜率为2.
,且斜率为2.
(1)求双曲线的方程;
(2)若切线与双曲线的切点为![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
解法1 设双曲线方程为![]() .
.
由于其与直线![]() ,即
,即![]() 相切,
相切,
则联立方程组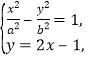 只有唯一一组解.
只有唯一一组解.
故关于![]() 的方程
的方程![]() ①有两个相等的实根,其判别式
①有两个相等的实根,其判别式![]() ,即
,即
![]() .②
.②
由双曲线的两个焦点坐标得其半焦距为![]() .
.
则![]() .
.
与式②联立解得![]() ,
,![]() .
.
因此,双曲线方程为![]() ,且式①关于
,且式①关于![]() 的方程变为
的方程变为
![]() .
.
代入![]() ,得
,得![]() .
.
这表明,切点![]() .
.
因此,直线![]() 的斜率为
的斜率为![]() ,其中,
,其中,![]() 是切线
是切线![]() 的斜率.
的斜率.
又点![]() 与
与![]() 的横坐标相同,则
的横坐标相同,则
![]() 轴
轴![]() .
.
解法2 设双曲线方程为![]() .
.
由半焦距![]() ,知
,知![]() .
.
又设点![]() .则过
.则过![]() 的切线方程为
的切线方程为![]() .
.
与所给的切线方程![]() ,即
,即![]() 比较知
比较知![]() ,
,![]() .
.
将其代入![]() ,得
,得![]() .
.
与![]() 联立解得
联立解得![]() ,
,![]() .
.
因此,双曲线的方程为![]() .
.
从而,切点坐标为![]() .
.
余下同解法1.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目