Question

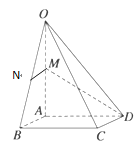
【题目】（题文）如图，长方形材料中，已知，.点为材料内部一点，于，于，且，. 现要在长方形材料中裁剪出四边形材料，满足，点、分别在边，上.

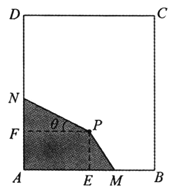
（1）设，试将四边形材料的面积表示为的函数，并指明的取值范围；

（2）试确定点在上的位置，使得四边形材料的面积最小，并求出其最小值.

Answer 1

【答案】(1)见解析;(2)当时，四边形材料的面积最小，最小值为.

【解析】分析：（1）通过直角三角形的边角关系，得出和，进而得出四边形材料的面积的表达式，再结合已知尺寸条件，确定角的范围.

（2）根据正切的两角差公式和换元法，化简和整理函数表达式，最后由基本不等式，确定面积最小值及对应的点在上的位置.

详解：解：（1）在直角中，因为，，

所以，

所以，

在直角中，因为，，

所以，

所以，

所以 ，.

（2）因为 ，

令，由，得，

所以 ，

当且仅当时，即时等号成立，

此时，，，

答：当时，四边形材料的面积最小，最小值为.