题目内容
【题目】如图,在几何体P﹣ABCD中,平面ABCD⊥平面PAB ,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.

(1)求证:EF∥平面PCD;
(2)求直线DP与平面ABCD所成角的正弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)根据EF是△BDP的中位线可知EF∥DP,即可利用线线平行得出线面平行;(2) 取AB中点O,连接PO,DO,可证明∠PDO为DP与平面ABCD所成角,在Rt△DOP中求解即可.
(1)因为E为AC中点,所以DB与AC交于点E.
因为E,F分别为AC,BP中点,所以EF是△BDP的中位线,
所以EF∥DP.又DP平面PCD,EF平面PCD,所以EF∥平面PCD.
(2)取AB中点O,连接PO,DO
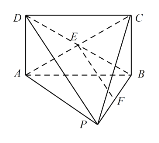
∵△PAB为正三角形,∴PO⊥AB,
又∵平面ABCD⊥平面PAB
∴PO⊥平面ABCD,∴DP在平面ABCD内的射影为DO,
∠PDO为DP与平面ABCD所成角,![]()
在Rt△DOP中,sin∠PDO=![]() ,
,
∴直线DP与平面ABCD所成角的正弦值为![]()

练习册系列答案
相关题目