题目内容
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() 且
且![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在定义域
在定义域![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据新定义的“局部对称点”的概念,计算![]() ,可得结果.
,可得结果.
(2)根据“局部对称点”的概念,利用分离参数的方法,可得![]() ,然后构造新函数,研究新函数的值域与
,然后构造新函数,研究新函数的值域与![]() 的关系,可得结果.
的关系,可得结果.
(3)根据“局部对称点”的概念,以及换元法,可得![]() 在
在![]() 有解然后构造函数
有解然后构造函数![]() ,利用函数性质,可得结果.
,利用函数性质,可得结果.
(1)由![]()
得![]() ,
,
代入![]() 得,
得,
![]() ,
,
得到关于![]() 的方程
的方程![]() ,
,![]() ,
,
则函数![]() 必有局部对称点.
必有局部对称点.
(2)方程![]() 在区间
在区间![]() 上有解
上有解
则![]() ,设
,设![]() ,
,
![]() ,
,![]() ,其中
,其中![]() ,
,
所以![]() .
.
(3)![]() ,
,
由于![]() ,所以
,所以
![]() ,
,
则![]()
所以可知方程![]() 在
在![]() 上有解,
上有解,
令![]() ,则
,则![]() ,
,
解法1:当![]() 时,
时,
由![]() ,可得
,可得
![]() .
.
![]() ,则
,则![]() ,
,
从而![]() 在
在![]() 有解
有解
即可保证![]() 为“局部奇函数”.
为“局部奇函数”.
令![]() ,
,
![]() 当
当![]() ,
,
![]() 在
在![]() 有解,
有解,
由![]() ,即
,即![]() ,
,
解得![]() ;
;
![]() 当
当![]() 时,
时,
![]() 在
在![]() 有解
有解
等价于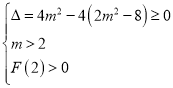 ,
,
解得![]() .
.
综上,所求实数![]() 的取值范围为
的取值范围为![]() .
.
解法2:方程![]() 变为
变为![]()
在区间![]() 内有解,其中一个根为
内有解,其中一个根为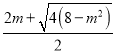
需满足条件:
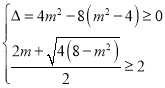 ,
,
即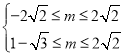 ,
,
化简得![]() .
.

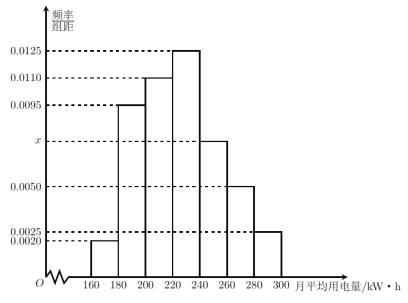
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:
收看时间(单位:小时) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
收看人数 | 14 | 30 | 16 | 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:
男 | 女 | 合计 | |
体育达人 | 40 | ||
非体育达人 | 30 | ||
合计 |
并判断能否有90%的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.求抽取的这两人恰好是一男一女的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()