题目内容
【题目】已知![]() (
(![]() 且
且![]() )是R上的奇函数,且
)是R上的奇函数,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于x的方程![]() 在区间
在区间![]() 内只有一个解,求m的取值集合;
内只有一个解,求m的取值集合;
(3)设![]() ,记
,记![]() ,是否存在正整数n,使不得式
,是否存在正整数n,使不得式![]() 对一切
对一切![]() 均成立?若存在,求出所有n的值,若不存在,说明理由.
均成立?若存在,求出所有n的值,若不存在,说明理由.
【答案】(1)![]() ;
;
(2)m的取值集合![]() 或
或![]() }
}
(3)存在,![]()
【解析】
(1)利用奇函数的性质得到关于实数k的方程,解方程即可,注意验证所得的结果;
(2)结合函数的单调性和函数的奇偶性脱去f的符号即可;
(3)可得![]() ,即可得:
,即可得:
![]() 即可.
即可.
(1)由奇函数的性质可得:
![]() ,解方程可得:
,解方程可得:![]() .
.
此时![]() ,满足
,满足![]() ,即
,即![]() 为奇函数.
为奇函数.
![]() 的解析式为:
的解析式为:![]() ;
;
(2)函数的解析式为:![]() ,
,
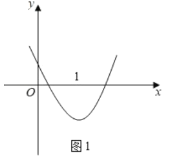
结合指数函数的性质可得:![]() 在区间
在区间![]() 内只有一个解.
内只有一个解.
即:![]() 在区间
在区间![]() 内只有一个解.
内只有一个解.
(i)当![]() 时,
时,![]() ,符合题意.
,符合题意.
(ii)当![]() 时,
时, ![]()
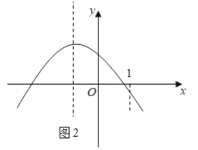
只需![]() 且
且![]()
![]() 时,
时,![]() ,此时
,此时![]() ,符合题意
,符合题意
综上,m的取值集合![]() 或
或![]() }
}
(3)![]() 函数
函数![]() 为奇函数
为奇函数
![]() 关于
关于![]() 对称
对称
![]()
![]()
又![]()
![]()
![]()
![]() 当且仅当
当且仅当![]() 时等号成立
时等号成立
![]()
所以存在正整数n,使不得式![]() 对一切
对一切![]() 均成立.
均成立.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目