题目内容
7.在△ABC中,AB=1,AC=2,∠A=120°,点O是△ABC的外心,存在实数λ,μ,使$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则( )| A. | λ=$\frac{5}{4}$,μ=$\frac{3}{4}$ | B. | λ=$\frac{4}{3}$,μ=$\frac{5}{6}$ | C. | λ=$\frac{5}{3}$,μ=$\frac{7}{6}$ | D. | λ=$\frac{4}{3}$,μ=$\frac{3}{4}$ |
分析 如图所示,过点O分别作OD⊥AB,OE⊥AC,D,E分别垂足.$\overrightarrow{AB}$•$\overrightarrow{AC}$=-1.由$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$=$\frac{1}{2}$,$\overrightarrow{AO}•\overrightarrow{AB}$=λ-μ
,可得λ-μ=$\frac{1}{2}$.同理可得:-λ+4μ=2.联立解出即可.
解答 解:如图所示,过点O分别作OD⊥AB,OE⊥AC,D,E分别垂足.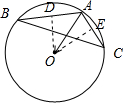
$\overrightarrow{AB}$•$\overrightarrow{AC}$=1×2×cos120°=-1
$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$=$\frac{1}{2}$,$\overrightarrow{AO}•\overrightarrow{AB}$=λ-μ
∴λ-μ=$\frac{1}{2}$.
同理可得:-λ+4μ=2.
联立解得λ=$\frac{4}{3}$,μ=$\frac{5}{6}$.
故选B.
点评 本题考查了向量共线定理、圆的垂经定理、数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
17.下列命题错误的是( )
| A. | 命题“?x∈R,x2-x+1≥$\frac{3}{4}$”的否定是“?x0∈R,x02-x0+1<$\frac{3}{4}$” | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| C. | 命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | |
| D. | 若命题“非p”与命题“p或q”都是真命题,那么q一定是假命题 |
19.设S是整数集Z的非空子集,如果?a,b∈Z,都有a2-b2∈S,则称S是一个好集,已知S是一个“好集”,下面命题为假命题的是( )
| A. | 一切奇数都属于S | B. | 偶数4k-2(k∈Z)都不属于S | ||
| C. | 若x,y∈S,则xy∈S | D. | 若x,y属于S,则x+y∈S |
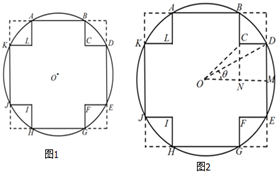 如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)
如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)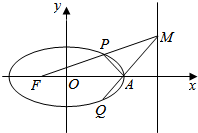 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左焦点为F(-1,0),M为右准线x=4上的一动点(不在x轴上),线段FM交椭圆于点P,MA与椭圆的另一交点为Q.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左焦点为F(-1,0),M为右准线x=4上的一动点(不在x轴上),线段FM交椭圆于点P,MA与椭圆的另一交点为Q.