题目内容
2.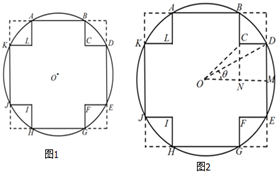 如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)
如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)(1)若要使截出的“十字形”的边长相等(DE=CD)(图1),此时边长为多少?
(2)若要使截出的“十字形”的面积为最大(图2),此时∠DOE为多少?(用反三角函数表示)
分析 (1)当“十字形”的边长相等时,过O作OM⊥DE交DE于E,作CN⊥OM交OM于N.设该“十字形”的边长为2x,则DM=x,OM=3x.在Rt△OMD中,由勾股定理得边长;
(2)过O作OM⊥DE交DE于E,作CN⊥OM交OM于N,求出面积,即可得出结论.
解答 解:(1)当“十字形”的边长相等时,过O作OM⊥DE交DE于E,作CN⊥OM交OM于N.设该“十字形”的边长为2x,则DM=x,OM=3x.
在Rt△OMD中,由勾股定理得,x2+(3x)2=25,可得x=$\frac{\sqrt{10}}{2}$…5分
所以,边长2x=$\sqrt{10}$cm…6分
(2)过O作OM⊥DE交DE于E,作CN⊥OM交OM于N.设∠DOM=θ,则OM=5cosθ,DM=5sinθ.
∴ON=CN=5sinθ,NM=5cosθ-5sinθ.…8分
∴“十字形”的面积为S=(2OM)2-4(NM)2=100cos2θ-100(cosθ-sinθ)2=$100(\frac{{\sqrt{5}}}{2}sin(2θ+φ)-\frac{1}{2})$( 其中$cosφ=\frac{{2\sqrt{5}}}{5}$或$tanϕ=\frac{1}{2}$) $({0<θ<\frac{π}{2}})$…10分
∴当$2θ+ϕ=\frac{π}{2}$时,${S_{max}}=50({\sqrt{5}-1})\;c{m^2}$…12分
此时,$∠DOE=2θ=\frac{π}{2}-arccos\frac{{2\sqrt{5}}}{5}$或$\frac{π}{2}-arctan\frac{1}{2}$…14分.
点评 本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.要得到y=cos2x的图象,可由函数y=cos(2x-$\frac{π}{3}$)的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
13.对于集合A、B,定义A+B={x+y|x∈A,y∈B},下列命题:
①A+B=B+A;
②(A+B)+C=A+(B+C);
③若A+A=B+B,则A=B;
④若A+C=B+C,则A=B.
其中正确的命题是( )
①A+B=B+A;
②(A+B)+C=A+(B+C);
③若A+A=B+B,则A=B;
④若A+C=B+C,则A=B.
其中正确的命题是( )
| A. | ① | B. | ①② | C. | ②③ | D. | ①④ |
17.有甲、乙两批种子,发芽率分别为0.8和0.9,在两批种子中各取一粒,则恰有一粒种子能发芽的概率是( )
| A. | 0.26 | B. | 0.08 | C. | 0.18 | D. | 0.72 |
7.在△ABC中,AB=1,AC=2,∠A=120°,点O是△ABC的外心,存在实数λ,μ,使$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则( )
| A. | λ=$\frac{5}{4}$,μ=$\frac{3}{4}$ | B. | λ=$\frac{4}{3}$,μ=$\frac{5}{6}$ | C. | λ=$\frac{5}{3}$,μ=$\frac{7}{6}$ | D. | λ=$\frac{4}{3}$,μ=$\frac{3}{4}$ |
14.设平面α⊥平面β,直线a?α,直线b?β,且a⊥b,则( )
| A. | a⊥β | B. | b⊥α | ||
| C. | a⊥β与b⊥α中至少有一个成立 | D. | a⊥β与b⊥α同时成立 |
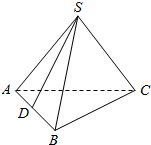 如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.
如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.