题目内容
17.下列命题错误的是( )| A. | 命题“?x∈R,x2-x+1≥$\frac{3}{4}$”的否定是“?x0∈R,x02-x0+1<$\frac{3}{4}$” | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| C. | 命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | |
| D. | 若命题“非p”与命题“p或q”都是真命题,那么q一定是假命题 |
分析 A.根据含有量词的命题的否定进行判断.
B.根据逆否命题的定义进行判断.
C.根据命题的否命题的定义进行判断.
D.根据复合命题真假之间的关系进行判断即可.
解答 解:A.命题“?x∈R,x2-x+1≥$\frac{3}{4}$”的否定是“?x0∈R,x02-x0+1<$\frac{3}{4}$”,故A正确,
B.命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”,故B正确,
C.命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0,故C正确,
D.若命题“非p”为真命题,则p为假命题,若命题“p或q”都是真命题,则q为真命题,故D错误,
故选:D
点评 本题主要考查命题的真假判断,涉及的知识点有含有量词的命题的否定,以及四种命题之间的关系.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
7.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
12.要得到y=cos2x的图象,可由函数y=cos(2x-$\frac{π}{3}$)的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
7.在△ABC中,AB=1,AC=2,∠A=120°,点O是△ABC的外心,存在实数λ,μ,使$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则( )
| A. | λ=$\frac{5}{4}$,μ=$\frac{3}{4}$ | B. | λ=$\frac{4}{3}$,μ=$\frac{5}{6}$ | C. | λ=$\frac{5}{3}$,μ=$\frac{7}{6}$ | D. | λ=$\frac{4}{3}$,μ=$\frac{3}{4}$ |
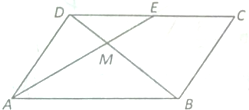
 在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.
在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.