题目内容
18.求函数f(x)=x2-2ax在[-1,0]上的最大值M(a)和最小值m(a)分析 由条件可得f(x)=x2-2ax的图象的对称轴方程为x=a,再利用二次函数的性质,分类讨论求得函数在[-1,0]上的最大值M(a)和最小值m(a).
解答 解:函数f(x)=x2-2ax的图象的对称轴方程为x=a,
①当a<-1时,函数f(x)=x2-2ax在[-1,0]上单调递增,
故函数f(x)的最大值M(a)=f(0)=0,最小值m(a)=f(-1)=1+2a.
②当-1≤a<-1212时,函数f(x)的最大值M(a)=f(0)=0,最小值m(a)=f(a)=-a2.
③当-1212≤a≤0时,函数f(x)的最大值M(a)=f(-1)=1+2a,最小值m(a)=f(a)=-a2.
④当a>0时,函数f(x)=x2-2ax在[-1,0]上单调递减,
故函数f(x)的最大值M(a)=f(-1)=1+2a,最小值m(a)=f(0)=0.
点评 本题主要考查二次函数的性质应用,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
13.对于集合A、B,定义A+B={x+y|x∈A,y∈B},下列命题:
①A+B=B+A;
②(A+B)+C=A+(B+C);
③若A+A=B+B,则A=B;
④若A+C=B+C,则A=B.
其中正确的命题是( )
①A+B=B+A;
②(A+B)+C=A+(B+C);
③若A+A=B+B,则A=B;
④若A+C=B+C,则A=B.
其中正确的命题是( )
| A. | ① | B. | ①② | C. | ②③ | D. | ①④ |
7.在△ABC中,AB=1,AC=2,∠A=120°,点O是△ABC的外心,存在实数λ,μ,使→AO−−→AO=λ→AB−−→AB+μ→AC−−→AC,则( )
| A. | λ=5454,μ=3434 | B. | λ=4343,μ=5656 | C. | λ=5353,μ=7676 | D. | λ=4343,μ=3434 |
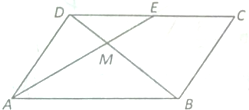
 在四边形ABCD中,AB=
在四边形ABCD中,AB=