题目内容
16.在△ABC中,AB=2,BC=3,D是三角形内一点,CD=2,使∠B+∠ADC=180°,问求当∠B为何值时,△ABC和△ADC面积之差最大?(∠B=$\frac{π}{4}$时,面积之差最大)分析 求出S△ABC=$\frac{1}{2}×2×3$sinB=3sinB,再求出AD=-4cosB+3,则可求出两三角形的面积差表达式为4cosBsinB=2sin2B,即可得出结论.
解答 解:根据正弦定理知S△ABC=$\frac{1}{2}×2×3$sinB=3sinB
根据余弦定理可知AC2=13-12cosB
且可知AD2+CD2+2AD•CD•cosB=AC2,
联立求出AD=-4cosB+3,
则可求出两三角形的面积差表达式为4cosBsinB=2sin2B≤2
当且仅当B=45°时,取等号,
所以B=45°时,面积之差最大.
点评 这题主要考查余弦定理,利用已知两边和夹角求第三边与面积,另外还设计了一元二次方程的求根方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.在△ABC中,AB=1,AC=2,∠A=120°,点O是△ABC的外心,存在实数λ,μ,使$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则( )
| A. | λ=$\frac{5}{4}$,μ=$\frac{3}{4}$ | B. | λ=$\frac{4}{3}$,μ=$\frac{5}{6}$ | C. | λ=$\frac{5}{3}$,μ=$\frac{7}{6}$ | D. | λ=$\frac{4}{3}$,μ=$\frac{3}{4}$ |
4.做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的高与底面直径的比为( )
| A. | $\frac{a}{b}$ | B. | $\frac{{a}^{2}}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{{b}^{2}}{a}$ |
7.与双曲线x2-2y2=2有相同渐近线,且过点M(2,-2)的双曲线的标准方程( )
| A. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{4}$=1或$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 | ||
| C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{4}$=1 |
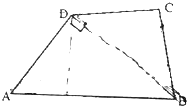 在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.
在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n. 如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.
如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.