题目内容
【题目】设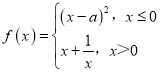
．
（1）当
时，f（x）的最小值是_____；
（2）若f（0）是f（x）的最小值，则a的取值范围是_____．
【答案】
[0，
]
【解析】
（1）先求出分段函数的每一段的最小值，再求函数的最小值；（2）对
分两种情况讨论，若a＜0，不满足条件．若a≥0，f（0）＝a2≤2，即0≤a
，即得解.
（1）当
时，当x≤0时，f（x）＝（x
）2≥（）2
，
当x＞0时，f（x）＝x
2
2，当且仅当x＝1时取等号，
则函数的最小值为
，
（2）由（1）知，当x＞0时，函数f（x）≥2，此时的最小值为2，
若a＜0，则当x＝a时，函数f（x）的最小值为f（a）＝0，此时f（0）不是最小值，不满足条件．
若a≥0，则当x≤0时，函数f（x）＝（x﹣a）2为减函数，
则当x≤0时，函数f（x）的最小值为f（0）＝a2，
要使f（0）是f（x）的最小值，则f（0）＝a2≤2，即0≤a，
即实数a的取值范围是[0，
]
练习册系列答案
天天向上口算本系列答案
相关题目
