题目内容
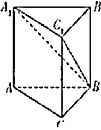
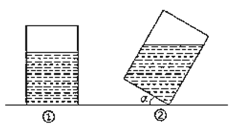
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
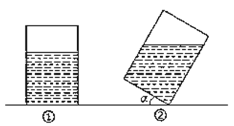
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
【答案】(1)要使倾斜后容器内的溶液不会溢出,![]() 的最大值是45°(2)不能实现要求,详见解析
的最大值是45°(2)不能实现要求,详见解析
【解析】
(1)当倾斜至上液面经过点B时,容器内溶液恰好不会溢出,此时![]() 最大.
最大.
(2)当![]() 时,设剩余的液面为
时,设剩余的液面为![]() ,比较
,比较![]() 与60°的大小后发现
与60°的大小后发现![]() 在
在![]() 上,计算此时倒出的液体体积,比
上,计算此时倒出的液体体积,比![]() 小,从而得出结论.
小,从而得出结论.
(1)如图③,当倾斜至上液面经过点B时,容器内溶液恰好不会溢出,此时![]() 最大.
最大.
解法一:此时,梯形![]() 的面积等于
的面积等于![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
即![]() ,解得
,解得![]() ,
,![]() .
.
所以,要使倾斜后容器内的溶液不会溢出,![]() 的最大值是45°.
的最大值是45°.
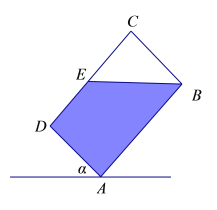
③
解法二:此时,![]() 的面积等于图①中没有液体部分的面积,即
的面积等于图①中没有液体部分的面积,即![]() ,
,
因为![]() ,所以
,所以![]()
![]()
,即![]() ,
,
解得![]() ,
,![]() .
.
所以,要使倾斜后容器内的溶液不会溢出,![]() 的最大值是45°.
的最大值是45°.
(2)如图④,当![]() 时,设上液面为
时,设上液面为![]() ,因为
,因为![]() ,所以点F在线段
,所以点F在线段![]() 上,
上,
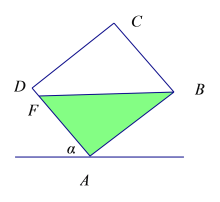
④
此时![]() ,
,![]() ,
,![]() ,
,
剩余溶液的体积为![]() ,
,
由题意,原来溶液的体积为![]() ,
,
因为![]() ,所以倒出的溶液不满
,所以倒出的溶液不满![]() .
.
所以,要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,不能实现要求.
时,不能实现要求.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目