Question

【题目】关于函数，下列判断正确的是（ ）

A.是的极大值点

B.函数有且只有1个零点

C.存在正实数，使得成立

D.对任意两个正实数，，且，若，则.

Answer 1

【答案】BD

【解析】

A.求函数的导数，结合函数极值的定义进行判断

B.求函数的导数，结合函数的单调性，结合函数单调性和零点个数进行判断即可

C.利用参数分离法，构造函数g（x），求函数的导数，研究函数的单调性和极值进行判断即可

D.令g（t）＝f（2+t）﹣f（2﹣t），求函数的导数，研究函数的单调性进行证明即可

A.函数的 的定义域为（0，+∞），

函数的导数f′（x），∴（0，2）上，f′（x）＜0，函数单调递减，（2，+∞）上，f′（x）＞0，函数单调递增，

∴x＝2是f（x）的极小值点，即A错误；

B.y＝f（x）﹣xlnx﹣x，∴y′10，

函数在（0，+∞）上单调递减，且f（1）﹣1ln1﹣1=1>0，f（2）﹣2ln2﹣2= ln2﹣1<0，∴函数y＝f（x）﹣x有且只有1个零点，即B正确；

C.若f（x）＞kx，可得k，令g（x），则g′（x），

令h（x）＝﹣4+x﹣xlnx，则h′（x）＝﹣lnx，

∴在x∈（0，1）上，函数h（x）单调递增，x∈（1，+∞）上函数h（x）单调递减，

∴h（x）h（1）＜0，∴g′（x）＜0，

∴g（x）在（0，+∞）上函数单调递减，函数无最小值，

∴不存在正实数k，使得f（x）＞kx恒成立，即C不正确；

D.令t∈（0，2），则2﹣t∈（0，2），2+t＞2，

令g（t）＝f（2+t）﹣f（2﹣t）ln（2+t）ln（2﹣t）ln，

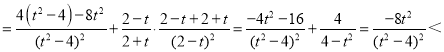则g′（t）0，

∴g（t）在（0，2）上单调递减，

则g（t）＜g（0）＝0，

令x1＝2﹣t，

由f（x1）＝f（x2），得x2＞2+t，

则x1+x2＞2﹣t+2+t＝4，

当x2≥4时，x1+x2＞4显然成立，

∴对任意两个正实数x1，x2，且x2＞x1，若f（x1）＝f（x2），则x1+x2＞4，故D正确

故正确的是BD，

故选：BD．