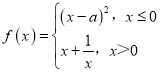题目内容
【题目】已知数列![]() 的首项
的首项![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,数列
,数列![]() 是公比不为
是公比不为![]() 的等比数列.
的等比数列.
(1)求实数![]() 的值;
的值;
(2)设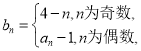 数列
数列![]() 的前
的前![]() 项和为
项和为![]() ,求所有正整数
,求所有正整数![]() 的值,使得
的值,使得![]() 恰好为数列
恰好为数列![]() 中的项.
中的项.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据递推公式求出![]() 、
、![]() ,由题意得出
,由题意得出![]() ,求出
,求出![]() 的值,结合数列
的值,结合数列![]() 公比不为
公比不为![]() 的等比数列进行检验,进而得出实数
的等比数列进行检验,进而得出实数![]() 的值;
的值;
(2)求出 利用奇偶分组法求出
利用奇偶分组法求出![]() 、
、![]() ,设
,设![]() ,可得知
,可得知![]() ,从而可知
,从而可知![]() 、
、![]() 或
或![]() 为偶数,由
为偶数,由![]() 结合
结合![]() 可推出
可推出![]() 不成立,然后分
不成立,然后分![]() 和
和![]() 为偶数两种情况讨论,结合
为偶数两种情况讨论,结合![]() 的取值范围可求出符合条件的正整数
的取值范围可求出符合条件的正整数![]() 的值.
的值.
(1)由![]() ,
,![]() 可知,
可知,![]() ,
,![]() ,
,
因为![]() 为等比数列,所以
为等比数列,所以![]() ,
,
即![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以数列![]() 的公比为1,不符合题意;
的公比为1,不符合题意;
当![]() 时,
时,![]() ,所以数列
,所以数列![]() 的公比
的公比![]() ,
,
所以实数![]() 的值为
的值为![]() .
.
(2)由(1)知![]() ,所以
,所以
则![]()
![]()
![]() ,
,
则![]() ,
,
因为![]() ,又
,又![]() ,
,
且![]() ,
,![]() ,所以
,所以![]() ,则
,则![]() ,设
,设![]() ,
,
则![]() 或
或![]() 为偶数,因为
为偶数,因为![]() 不可能,所以
不可能,所以![]() 或
或![]() 为偶数,
为偶数,
①当![]() 时,
时,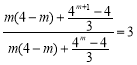 ,化简得
,化简得![]() ,
,
即![]() ,所以
,所以![]() 可取值为1,2,3,
可取值为1,2,3,
验证![]() ,
,![]() ,
,![]() 得,当
得,当![]() 时,
时,![]() 成立.
成立.
②当![]() 为偶数时,
为偶数时, ,
,
设![]() ,则
,则![]() ,
,
由①知![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ,
,
所以 ,令
,令![]() ,则
,则 ,
,
即![]() ,无整数解.
,无整数解.
综上,正整数![]() 的值为
的值为![]() .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】为检查某工厂所生产的8万台电风扇的质量,抽查了其中20台的无故障连续使用时限(单位:小时) 如下:
248 256 232 243 188 268 278 266 289 312
274 296 288 302 295 228 287 217 329 283
分组 | 频数 | 频率 | 频率/组距 |
| |||
| |||
| |||
| |||
| |||
| |||
| |||
| |||
总计 | 0.05 |
(1)完成频率分布表,并作出频率分布直方图;
(2)估计8万台电风扇中有多少台无故障连续使用时限不低于280小时;
(3)用组中值(同一组中的数据在该组区间的中点值)估计样本的平均无故障连续使用时限.
【题目】某种零件的质量指标值为整数,指标值为8时称为合格品,指标值为7或者9时称为准合格品,指标值为6或10时称为废品,某单位拥有一台制造该零件的机器,为了了解机器性能,随机抽取了该机器制造的100个零件,不同的质量指标值对应的零件个数如下表所示;
质量指标值 | 6 | 7 | 8 | 9 | 10 |
零件个数 | 6 | 18 | 60 | 12 | 4 |
使用该机器制造的一个零件成本为5元,合格品可以以每个![]() 元的价格出售给批发商,准合格品与废品无法岀售.
元的价格出售给批发商,准合格品与废品无法岀售.
(1)估计该机器制造零件的质量指标值的平均数;
(2)若该单位接到一张订单,需要该零件2100个,为使此次交易获利达到1400元,估计![]() 的最小值;
的最小值;
(3)该单位引进了一台加工设备,每个零件花费2元可以被加工一次,加工结果会等可能出现以下三种情况:①质量指标值增加1,②质量指标值不变,③质量指标值减少1.已知每个零件最多可被加工一次,且该单位计划将所有准合格品逐一加工,在(2)的条件下,估计![]() 的最小值(精确到0.01) .
的最小值(精确到0.01) .
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:![]() ,
,![]() ;
;![]()