题目内容
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
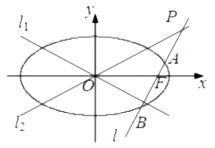
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),且直线
不重合),且直线![]() 与
与![]() 轴的交于点
轴的交于点![]() ,试问
,试问![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)1.
; (Ⅱ)1.
【解析】试题分析:(1)由椭圆C的左顶点A在圆x2+y2=12上,求得a,由椭圆的一个焦点得c=3,由b2=a2-c2得b,即可.
(2)由题意,N1(x2,-y2),可得直线NM的方程,令y=0,可得点P的坐标为(4,0). 利用△PMN的面积为S= ![]() |PF||y1-y2|,化简了基本不等式的性质即可得出.
|PF||y1-y2|,化简了基本不等式的性质即可得出.
试题解析:
(Ⅰ)∵椭圆![]() 的左顶点
的左顶点![]() 在圆
在圆![]() 上,∴
上,∴![]()
又∵椭圆的一个焦点为![]() ,∴
,∴![]() ∴
∴![]()
∴椭圆![]() 的方程为
的方程为![]()
(Ⅱ)设![]() ,则直线与椭圆
,则直线与椭圆![]() 方程联立
方程联立
化简并整理得![]() ,
,
∴![]() ,
, ![]()
由题设知![]() ∴直线
∴直线![]() 的方程为
的方程为![]()
令![]() 得
得![]()
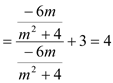 ∴点
∴点![]()
![]()
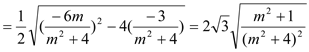
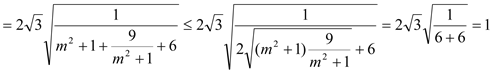
(当且仅当![]() 即
即![]() 时等号成立)
时等号成立)
∴![]() 的面积存在最大值,最大值为1.
的面积存在最大值,最大值为1.

练习册系列答案
相关题目