题目内容
【题目】若函数
在区间
上， 
， 
， 
， 
， 
， 
均可为一个三角形的三边长，则称函数
为“三角形函数”．已知函数
在区间
上是“三角形函数”，则实数
的取值范围为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】试题分析：根据“三角形函数”的定义可知，若
在区间
上的“三角形函数”，则
在
上的最大值和最小值应满足
，由
可得
，所以
在
上单调递减，在
上单调递增， 
，所以
，解得
的取值范围为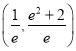
，故选A.
【方法点睛】本题主要考查了利用导数研究函数在闭区间上的最值，考查考生应用所学知识解决问题的能力，属于中档题.解答本题首先通过给出的定义把问题转化为函数的最值问题，通过导数研究其单调性，得到最小值，通过比较区间端点的函数值求出最大值，列出关于参数
的不等式，进而求得其范围.
练习册系列答案
相关题目
