题目内容
10.已知向量$\overrightarrow{a}=(sinθ,cosθ)$,$\overrightarrow{b}$=(3,4),若$\overrightarrow{a}⊥\overrightarrow{b}$,则tanθ等于( )| A. | $-\frac{24}{7}$ | B. | $\frac{6}{7}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{4}{3}$ |
分析 由向量的垂直关系和同角三角函数的基本关系可得.
解答 解:∵向量$\overrightarrow{a}=(sinθ,cosθ)$,$\overrightarrow{b}$=(3,4),
由$\overrightarrow{a}⊥\overrightarrow{b}$可得$\overrightarrow{a}$•$\overrightarrow{b}$=3sinθ+4cosθ=0,
∴tanθ=$\frac{sinθ}{cosθ}$=-$\frac{4}{3}$
故选:D
点评 本题考查平面向量的数量积和垂直关系,属基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
15.已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+1的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | $[-\frac{5}{4},+∞)$ | B. | [1,2] | C. | $[-\frac{5}{4},1]$ | D. | [-1,1] |
20.将函数f(x)=sin2x的图象向左平移$\frac{π}{4}$个长度单位,得到函数g(x)的图象,则g(x)的单调递增区间是( )
| A. | (kπ-$\frac{π}{2}$,kπ)(k∈Z) | B. | (kπ,kπ+$\frac{π}{2}$)(k∈Z) | C. | (kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$)(k∈Z) | D. | (kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$)(k∈Z) |
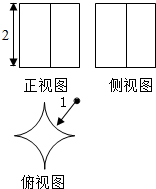 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.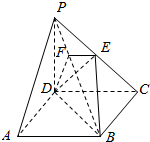 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.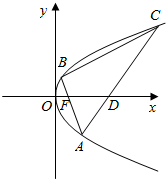 已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.
已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.