题目内容
18.数列{an}的前n项和为Sn,已知a1=2,且${S_{n-1}}={a_n}(n≥2,n∈{N^*})$.(1)求a2,a3,a4;
(2)猜想{an}的通项公式,并用数学归纳法证明.
分析 (1)由已知条件分别取n=2,3,4,能依次求出a2,a3,a4的值.
(2)猜想${a}_{n}=\left\{\begin{array}{l}{2,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$,当n=1时,和n=2时,验证猜想成立,然后假设n=k时,猜想成立,由此推导出当n=k+1时,猜想成立,由此能证明${a}_{n}=\left\{\begin{array}{l}{2,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$.
解答 解:(1)∵数列{an}的前n项和为Sn,a1=2,且${S_{n-1}}={a_n}(n≥2,n∈{N^*})$.
∴a2=S1=a1=2,
a3=S2=2+2=4,
a4=S3=2+2+4=8.
(2)由a1=2,a2=2,a3=4,a4=8,猜想${a}_{n}=\left\{\begin{array}{l}{2,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$.
①当n=1时,a1=2;当n=2时,a2=2,成立.
②假设n=k时,成立,即${a}_{k}={2}^{k-1}$,k≥2,
则当n=k+1时,ak+1=Sk=2+2+4+8+…+2k-1=2+$\frac{2(1-{2}^{k-1})}{1-2}$=2k,成立,
由①②,得${a}_{n}=\left\{\begin{array}{l}{2,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$.
点评 本题考查数列的前四项的求法,考查数列的通项公式的猜想和证明,是中档题,解题时要认真审题,注意递推思想和数学归纳法的合理运用.

练习册系列答案
相关题目
6.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(其中ω>0)的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,把函数f(x)的图象沿x轴向左平移$\frac{π}{6}$个单位得到函数g(x)的图象,则g(x)的单调递减区间是( )
| A. | [kπ,$\frac{π}{2}$+kπ],k∈Z | B. | [-$\frac{π}{2}$+kπ,kπ],k∈Z | ||
| C. | [-$\frac{π}{4}$+kπ,$\frac{π}{4}$+kπ],k∈Z | D. | [$\frac{π}{4}$+kπ,$\frac{3π}{4}$+kπ],k∈Z |
13.已知U={1,2,3,4,5,6,7,8},A={1,3,5,7},B={2,5},则∁U(A∪B)等于( )
| A. | {6,8} | B. | {5,7} | C. | {4,6,8} | D. | {1,3,5,6,8} |
10.已知向量$\overrightarrow{a}=(sinθ,cosθ)$,$\overrightarrow{b}$=(3,4),若$\overrightarrow{a}⊥\overrightarrow{b}$,则tanθ等于( )
| A. | $-\frac{24}{7}$ | B. | $\frac{6}{7}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{4}{3}$ |
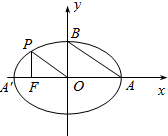 如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为$\frac{\sqrt{2}}{2}$.
如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为$\frac{\sqrt{2}}{2}$.