题目内容
2.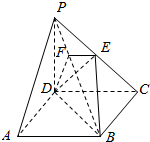 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.(1)求证:PA∥平面EDB;
(2)求证:PB⊥平面EFD;
(3)在线段AB上是否存在点M,使PM与平面PDB所成角的正弦值为$\frac{{\sqrt{38}}}{19}$?若存在,求出AM的长;若不存在,请说明理由.
分析 (1)由题意连接AC,AC交BD于O,连接EO,则EO是中位线,证出PA∥EO,由线面平行的判定定理知PA∥平面EDB;
(2)由PD⊥底面ABCD,得PD⊥DC,再由DC⊥BC证出BC⊥平面PDC,即得BC⊥DE,再由ABCD是正方形证出DE⊥平面PBC,则有DE⊥PB,再由条件证出PB⊥平面EFD;
(3)以D点为原点建立如图所示的直角坐标系,得到D,P,A,B的坐标,设出M的坐标,进一步得到所用向量的坐标,然后结合PM与平面PDB所成角的正弦值为$\frac{{\sqrt{38}}}{19}$求得M的坐标,说明结论成立,并求出AM的长.
解答 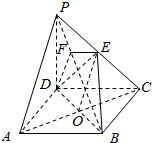 (1)证明:如图所示,连接AC,AC交BD于点O,连接EO.
(1)证明:如图所示,连接AC,AC交BD于点O,连接EO.
∵底面ABCD是正方形,∴点O是AC的中点.
在△PAC中,EO是中位线,∴PA∥EO.
而EO?平面EDB且PA?平面EDB,
∴PA∥平面EDB;
(2)证明:∵PD⊥底面ABCD,且DC?平面ABCD,∴PD⊥DC.
∵PD=DC,∴△PDC是等腰直角三角形.
又DE是斜边PC的中线,∴DE⊥PC.①
由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,∴DC⊥BC.
又PD∩DC=D,∴BC⊥平面PDC.
又DE?平面PDC,∴BC⊥DE.②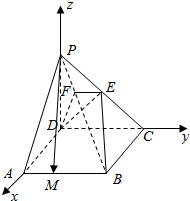
由①和②推得DE⊥平面PBC.
而PB?平面PBC,∴DE⊥PB.
又EF⊥PB,且DE∩EF=E,∴PB⊥平面EFD;
(3)解:以D点为原点建立如图所示的直角坐标系
设M点坐标为(1,a,0)(0≤a≤1),则D(0,0,0),P(0,0,1),A(1,0,0),B(1,1,0),
则$\overrightarrow{PD}=(0,0,-1),\overrightarrow{DB}=(1,1,0)$,$\overrightarrow{PM}=({1,a,-1})$.
设平面PDB的一个法向量为$\overrightarrow{n}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PD}=-z=0}\\{\overrightarrow{n}•\overrightarrow{DB}=x+y=0}\end{array}\right.$,取y=-1,得$\overrightarrow{n}=(1,-1,0)$.
由|$\frac{\overrightarrow{n}•\overrightarrow{PM}}{|\overrightarrow{n}||\overrightarrow{PM}|}$|=|$\frac{1-a}{\sqrt{2}•\sqrt{{a}^{2}+2}}$|=$\frac{\sqrt{38}}{19}$,解得:a=$\frac{1}{3}$或a=$\frac{11}{5}$(舍).
∴在线段AB上存在点M,使PM与平面PDB所成角的正弦值为$\frac{{\sqrt{38}}}{19}$,此时AM=$\frac{1}{3}$.
点评 本题考查了线线、线面平行和垂直的相互转化,通过中位线证明线线平行,再由线面平行的判定得到线面平行;垂直关系的转化是由线面垂直的定义和判定定理实现,训练了利用空间向量求线面角,是中档题.

| A. | {6,8} | B. | {5,7} | C. | {4,6,8} | D. | {1,3,5,6,8} |
| A. | $-\frac{24}{7}$ | B. | $\frac{6}{7}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{4}{3}$ |
| A. | 25 | B. | 16 | C. | 9 | D. | 4 |
| A. | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{6}=1$ | C. | $\frac{y^2}{6}-\frac{x^2}{3}=1$ | D. | $\frac{x^2}{6}-\frac{y^2}{3}=1$ |
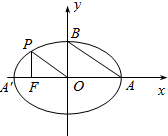 如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为$\frac{\sqrt{2}}{2}$.
如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为$\frac{\sqrt{2}}{2}$.