题目内容
20.将函数f(x)=sin2x的图象向左平移$\frac{π}{4}$个长度单位,得到函数g(x)的图象,则g(x)的单调递增区间是( )| A. | (kπ-$\frac{π}{2}$,kπ)(k∈Z) | B. | (kπ,kπ+$\frac{π}{2}$)(k∈Z) | C. | (kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$)(k∈Z) | D. | (kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$)(k∈Z) |
分析 先根据函数图象平移的原则,求出函数的解析式,再利用余弦函数的单调性,即可得到结论.
解答 解:函数y=sin2x的图象向左平移$\frac{π}{4}$个单位得y=sin(2x+$\frac{π}{2}$),即y=cos2x的图象,
由-π+2kπ<2x<2kπ(k∈Z),可得-$\frac{π}{2}$+kπ<x<kπ(k∈Z),
即所得函数的单调递增区间是:(kπ-$\frac{π}{2}$,kπ)(k∈Z).
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换,考查函数的性质,属于基础题.

练习册系列答案
相关题目
10.已知向量$\overrightarrow{a}=(sinθ,cosθ)$,$\overrightarrow{b}$=(3,4),若$\overrightarrow{a}⊥\overrightarrow{b}$,则tanθ等于( )
| A. | $-\frac{24}{7}$ | B. | $\frac{6}{7}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{4}{3}$ |
8.设变量x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y-3≥0\\ 2x-y-3≤0\end{array}\right.$则目标函数z=2x+3y的最大值为( )
| A. | 7 | B. | 8 | C. | 22 | D. | 23 |
12.焦点为(0,±3),且与双曲线$\frac{x^2}{2}-{y^2}=1$有相同的渐近线的双曲线方程是( )
| A. | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{6}=1$ | C. | $\frac{y^2}{6}-\frac{x^2}{3}=1$ | D. | $\frac{x^2}{6}-\frac{y^2}{3}=1$ |
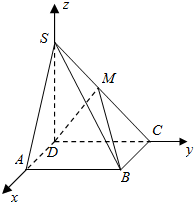 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M在侧棱SC上,∠ABM=60°.若以DA,DC,DS,分别为x轴,y轴,z轴建立如图所示的空间直角坐标系D-xyz,则M的坐标为(0,1,1).
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M在侧棱SC上,∠ABM=60°.若以DA,DC,DS,分别为x轴,y轴,z轴建立如图所示的空间直角坐标系D-xyz,则M的坐标为(0,1,1).