题目内容
15.若不等式组$\left\{\begin{array}{l}{x+y-1≥0}\\{ax-y+1≥0}\\{x-1≤0}\end{array}\right.$(a为常数)所表示的平面区域的面积为2,则a的值为3.分析 作出不等式组对应的平面区域,利用平面区域的形状,结合面积公式即可得到结论.
解答 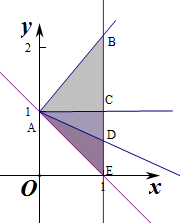 解:作出不等式组对应的平面区域:
解:作出不等式组对应的平面区域:
直线ax-y+1=0过定点A(0,1),
当a=0时,区域为△AEC,其中E(1,0),C(1,1),
则△AEC的面积S=$\frac{1}{2}×1×1=\frac{1}{2}$<2,
∴a>0,
由$\left\{\begin{array}{l}{x=1}\\{ax-y+1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1+a}\end{array}\right.$,
即B(1,1+a),
∵平面区域的面积是2,
∴$\frac{1}{2}$×(′1+a)×1=2,
即1+a=4,
解得a=3,
故答案为:3.
点评 作出不等式组对应的平面区域,利用平面区域的形状,结合面积公式即可得到结论.

练习册系列答案
相关题目
3.已知等比数列{an}中,a4+a8=$\frac{1}{2}$,则a6(a2+2a6+a10)的值为( )
| A. | 1 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
10.设m<0,-1<n<0,则m,mn,mn2三者的关系大小为( )
| A. | m<mn2<mn | B. | m<mn<mn2 | C. | mn2<m<mn | D. | mn2<mn<m |
 如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ过点C,其中AB=30米,AD=20米.记三角形花园APQ的面积为S.
如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ过点C,其中AB=30米,AD=20米.记三角形花园APQ的面积为S.