题目内容
【题目】已知一圆经过点
，
,且它的圆心在直线
上.
（I）求此圆的方程；
（II）若点
为所求圆上任意一点，且点
,求线段
的中点
的轨迹方程.
【答案】（1）（x﹣2）2+（y﹣4）2=10．（2）（x﹣
）2+（y﹣2）2=
【解析】
试题（1）首先设出方程，将点坐标代入得到关于参数的方程组，通过解方程组得到参数值，从而确定其方程；（2）首先设出点M的坐标，利用中点得到点D坐标，代入圆的方程整理化简得到的中点M的轨迹方程
试题解析：（Ⅰ）由已知可设圆心N（a，3a﹣2），又由已知得|NA|=|NB|， 从而有
，解得：a=2．
于是圆N的圆心N（2，4），半径
所以，圆N的方程为（x﹣2）2+（y﹣4）2=10．（6分）
（2）设M（x，y），D（x1，y1），则由C（3，0）及M为线段CD的中点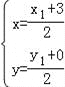得：
，解得：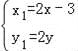
． 又点D在圆N：（x﹣2）2+（y﹣4）2=10上，所以有（2x﹣3﹣2）2+（2y﹣4）2=10，化简得：
故所求的轨迹方程为
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题．该企业为了检查生产该产品的甲，乙两条流水线的生产情况，随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本，测出它们的这一项质量指标值．若该项质量指标值落在
内，则为合格品，否则为不合格品．表1是甲流水线样本的频数分布表，图1是乙流水线样本的频率分布直方图．
（Ⅰ）根据图１，估计乙流水线生产产品该质量指标值的中位数；
（Ⅱ）若将频率视为概率，某个月内甲，乙两条流水线均生产了5000件产品，则甲，乙两条流水线分别生产出不合格品约多少件？
（Ⅲ）根据已知条件完成下面
列联表，并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲，乙两条流水线的选择有关”？
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附：
（其中
为样本容量）
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】今年年初，中共中央、国务院发布《关于开展扫黑除恶专项斗争的通知》，在全国范围部署开展扫黑除恶专项斗争.那么这次的“扫黑除恶”专项斗争与2000年、2006年两次在全国范围内持续开展了十多年的“打黑除恶”专项斗争是否相同呢？某高校一个社团在年后开学后随机调查了
位该校在读大学生，就“扫黑除恶”与“打黑除恶”是否相同进行了一次调查，得到具体数据如表：
不相同 | 相同 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
（1）根据如上的
列联表，能否在犯错误的概率不超过
的前提下，认为“扫黑除恶”与“打黑除恶”是否相同与性别有关"？
（2）计算这位大学生认为“扫黑除恶”与“打黑除恶”不相同的频率，并据此估算该校
名在读大学生中认为“扫黑除恶”与“打黑除恶”不相同的人数；
（3）为了解该校大学生对“扫黑除恶”与“打黑除恶”不同之处的知道情况，该校学生会组织部选取
位男生和
位女生逐个进行采访，最后再随机选取次采访记录放到该大学的官方网站上，求最后被选取的次采访对象中至少有一位男生的概率.
参考公式：
.
附表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】近期，某超市针对一款饮料推出刷脸支付活动，活动设置了一段时间的推广期，由于推广期内优惠力度较大，吸引越来越多的人开始使用刷脸支付.该超市统计了活动刚推出一周内每一天使用刷脸支付的人次，用
表示活动推出的天数，
表示每天使用刷脸支付的人次，统计数据如下表所示：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）在推广期内，
与
（
均为大于零的常数）哪一个适宜作为刷脸支付的人次关于活动推出天数的回归方程类型？（给出判断即可，不必说明理由）；
（2）根据（1）的判断结果及表
中的数据，求关于的回归方程，并预测活动推出第
天使用刷脸支付的人次；
（3）已知一瓶该饮料的售价为
元，顾客的支付方式有三种：现金支付、扫码支付和刷脸支付，其中有
使用现金支付，使用现金支付的顾客无优惠；有
使用扫码支付，使用扫码支付享受折优惠；有
使用刷脸支付，根据统计结果得知，使用刷脸支付的顾客，享受
折优惠的概率为
，享受折优惠的概率为
，享受
折优惠的概率为
.根据所给数据估计购买一瓶该饮料的平均花费.
参考数据：其中
，
|
|
|
|
|
|
参考公式：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计公式分别为：
.